Horizontales Federpendel mit Dämpfer, x(t) herleiten

Question

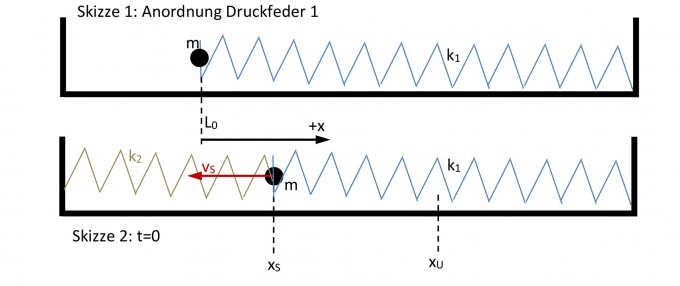
Es geht um ein gedämpftes, horizontales Federpendel mit einer Druckfeder 1.

Die Federkonstante von Feder 1 ist k₁ (siehe Skizze 1).

Skizze 2 zeigt die Anordnung für t=0.Die Masse m hat den Umkehrpunkt an der Stelle x_U hinter sich gelassen und bewegt sich auf die theoretische Ruhelage der Feder 1 zu.

Ab der Stelle x_S wirkt eine Druckfeder 2 als Dämpfer. Die Federkonstante sei k₂. Feder 2 ist vorgespannt. Die Länge der Vorspannung beträgt b₁.

Zum Zeitpunkt t = 0 befindet sich m an der Stelle x_S. Die Anfangsbedingungenen sind x(0) = x_S und v(0) = v_S, wobei v_S größer ist als im Normalfall, wenn das Federpendel sich selbst überlassen wäre.

Für Beschleunigung und Geschwindigkeit gilt:

$$a=\ddot x(t) bzw.v=\dot x(t)$$

aber mir ist nicht klar, wie man die überhöhte v_S berücksichtigt.

Mein Ansatz war: Auf m wirken zwei Kräfte, die Federkraft F₁ und die Federkraft F₂.

Wobei: Fres = F₁ + F₂

aus F = m a folgt a = F / m, somit:

$$\ddot x(t)=\frac{F_{1}+F_{2}}{m}$$

mit: F₁ = –k₁ x und F₂ = k₂ (b₁ + (x_s– x)) folgt:

$$\ddot x(t)=\frac{-k_{1}x(t)+k_{2}(b_{1}+x_{s}-x(t))}{m}$$

bzw.

$$\ddot x(t)+\frac{k_{1}+k_{2}}{m}x(t)=\frac{k_{2}}{m}(x_{s}+b_{1})$$

Dies führte zu x(t) + C₃ = C₁ cos (ωt) + C₂ sin (ωt) ≡ A cos (ωt + φ)

mit

$$C_{3}=\frac{k_{2}}{k_{1}+k_{2}}(b_{1}+x_{S})$$$$C_{2}=\frac{v_{S}}{\omega}$$

$$C_{1}=x_{S}+C_{3}+s_{1}$$

$$A=\sqrt{C_{1}^{2}+C_{2}^{2}}$$

 $$\varphi=arctan(\frac{-C_{2}}{C_{1}})$$

Es geht mir um die Herleitung von x(t) und v(t). Die Gegenprobe über den Energieansatz zeigt mir bisher, dass ich bei der Schwingungsgleichung einen falschen Ansatz verfolge. Vermutlich stoße ich an meine Grenzen...

Ich stehe hier vor mehreren Herausforderungen. Zum einen die erhöhte v_S und dann noch der Dämpfer.

Kann mir bitte jemand behilflich sein.

Comments

An voreilige Moderatoren: Bitte nicht in die Nanolounge verschieben. Der physikalische Hintergrund ist weitestgehend geklärt, es geht also fast nur noch um ein mathematisches Problem.

Und jetzt doch noch was Physikalisches: Fres = F1 + F2 stimmt nur, wenn man die Kräfte als Vektoren betrachtet. Sollte es nur um die Beträge gehen, musste  Fres = F1 - F2 verwendet werden.

---

Wieso nicht als Kommentar?

---

@ Risch

Wie bist du auf jeweils auf die Auslenkungen der Federn gekommen? Also Feder 1 : x
Feder 2: b1+(xs-x).

Answer 1

Vielen Dank für die Antworten.

Bzgl. der Auslenkungen: Die Feder 1 hatte ich als Referenz für den Nullpunkt angenommen. Ist Feder 1 im entspannten Zustand, hatte ich diese Stelle der Masse als Null angenommen. Davon ausgehend zählte ich die Auslenkung x der Feder 1.

Bei der Bewegung von Feder 2 ging ich von folgenden Annahmen aus: Bei t=0 ist sie vorgespannt (b1). An der Stelle x_S stößt die Masse auf Feder 2. Feder 2 wird noch weiter zusammengedrückt. Da sich zu t=0 die Masse in Richtung Nullpunkt bewegt, rechne ich für die zusätzliche Kompression der Feder 2 mit Kollisionspunkt minus der Bewegung von m: x_S-x. So komme ich auf die Kraft von Feder 2: k₂*(b₁ + (x_S-x)).

Wie eingangs kurz dargestellt, kam ich auf folgende Gleichungen:

$$x(t)=A cos(\omega t+\varphi)-C_{3}$$

$$v(t)=-A \omega sin(\omega t+\varphi)$$

Letztere liefert Momentangeschwindigkeiten, die laut Gegenrechnung über den Ansatz mittels Energie zu niedrig sind. Und nun meine Vermutung: die Störung durch v_S ist in meinem Ansatz nicht enthalten. Man kann es sich so vorstellen: Jemand hat die Masse des Federpendels von Hand in Richtung x gestoßen, es prallt vom Umkehrpunkt ab und kommt mit überhöhter Geschwindigkeit an der Stelle x_S an. Die Geschwindigkeit zu t=0 an x_S beträgt v_S. Der Betrag von v_S ist bekannt - ist somit nicht Teil der "Herausforderung".

Der Energieansatz ist gut für die Gegenprobe, aber für meine Analyse sind x(t) und v(t) erforderlich und ich bin dazu nicht in der Lage...

Comments

Kurz zur Skizze 1. Diese Skizze zeigt den eigentlichen horizontalen Federschwinger. Er besteht aus der Masse und Feder 1.

Feder 2 ist nicht mit der Masse verbunden. Erst an der Stelle x_S trifft die Masse m auf Feder 2, die als Dämpfer wirkt.

---

Die Frage befindet sich bereits in der nanolounge. Schaut bitte mal in beiden Lounges, ob das ein Duplikat ist. Link für Risch dürfte dann genügen.

PS. @mathelounge-beantworter: Es ist nicht verboten, eher erwünscht, dass ihr auch in der nanolounge Fragen beantwortet. Es gibt zeitnah einige recht genau formulierte Fragestellungen, die ihr mit etwas Aufwand bestimmt kompetent beantworten könntet.

---

dein Ansatz gilt ja nur, solange die masse in Kontakt mit k2 ist.

ohne k2 und vs, würde sich die Masse ja bei xs nach rechts bewegen,  was soll es also heissen, vs nach links und  ausserdem größer als v von m an k1 allein? von xs au nach links hat man einfach die Bewegung unter k1+k2 mit der Anfangsbedingung vs. für x rechts von xs hat man nur die Bewegung unter k1.

Kannst du bitte die Originalaufgabe posten?

---

Hallo lul,

korrekt, es geht ausschließlich um die Bewegung nach links, also während die Masse in Kontakt mit k₂ ist.

Es handelt sich um ein Problem aus der Praxis, das ich so gut es mir möglich ist zu beschreiben versuche. In Kurzform: Der Schwinger mit m und k₁ trifft mit Geschwindigkeit v_S auf eine Druckfeder k₂, die um b₁ vorgespannt ist.

Habe ich einen Fehler im Ansatz über die Energie? Nachfolgend steht S für Start, E=Ende, W=Spannarbeit:

$$E_{kinE}=E_{kinS}+W_{1}-W_{2}$$

$$\frac{m}{2}v_{E}^{2}=\frac{m}{2}v_{S}^{2}+\frac{k_{1}}{2}(x_{S}^{2}-x_{E}^{2})-\frac{k_{2}}{2}((b_{1}+(x_{S}-x_{E}))^{2}-b_{1}^{2})$$

$$v_{E}=\sqrt{v_{S}^{2}+\frac{k_{1}}{m}(x_{S}^{2}-x_{E}^{2})-\frac{k_{2}}{m}((b_{1}+x_{S}-x_{E})^{2}-b_{1}^{2})}$$

Als Ergebnis erhalte ich v_E= -2,142 m/s,

mit v_S= -2,19 m/s, k₁=432 N/m, k₂=600 N/m, m=0,357 kg,

x_S=0,0098 m, x_E=0,0081 m, b₁=0,042 m

---

Es hat funktioniert. Das Ergebnis über den Energieansatz war korrekt und inzwischen passt nun auch x(t). Vielen Dank an alle!