Hallo mistermathe! :-)
[...] und jetzt frage ich mich wie man in der Lösung hinbekommen hat die Krafteckte zu zeichnen, obwohl die Längen der jeweiligen Kontaktkräften unbekannt sind... Ich hoffe jemand kann mir die Lösungsschritte erklären. Was man machen muss um darauf zu kommen.
Die Beträge der Gewichtskräfte sind gegeben. Damit das Zeichnen der Kraftecke gelingt, muss erstmal das Freischneiden der Rohre gelingen. Sonst kann man alles in die Tonne hauen! Schneidest Du korrekt frei, sind die Wirklinien(bzw. Winkel) sowie die Richtungen aller Kräfte bedingt durch die Lage und der Durchmesser der Rohre bekannt. (Ich vermute einfach mal, dass die maßstäbliche Skizze mit dem Gerüst der Rohre gegeben ist, denn ich wüsste sonst nicht wie man die Aufgabe lösen könnte.) Gehen wir einfach davon aus, dass der Freischnitt fertig ist(Deine Frage bezieht sich ja aufs Zeichnen, nicht aufs Freischneiden.). Nun können wir beginnen, uns Teilsystem für Teilsystem, also Rohr für Rohr, an die Lösung heranzupirschen. (Ich schreibe gleich einen Vektor v ohne weitere Verzierungen und dessen Betrag als |v|.
Teilsystem 1.
Teilsystem 1 ist einfach. Wir kennen die Gewichtskraft Ga von Rohr A und die Wirklinien der Kräfte Ff und Fe und wir wissen, dass das Krafteck bei Kräftegleichgwicht bzw. im Zustand der Ruhe geschlossen ist. Also zeichnen wir einfach maßstäblich den Betrag der Kraft Ga in ihre vorbestimmte vertikale Richtung und durch die Spitze von Ga ziehen wir die Wirklinie von Fe beliebig lang, so wie es das Blatt Papier hergibt. Wir wissen ja, dass das Krafteck geschlossen sein muss, also zeichnen wir Ff horizontal so ein, dass die Spitze von Ff an den Anfang von Ga andockt und - zack - jetzt kennen wir die Beträge von Ff und Fe, indem wir ihre Längen messen und maßstabsgerecht umrechnen. Das System 1 ist hiermit abgehakt. Vielleicht noch eine Anmerkung: Die Reihenfolge wie die Kräfte bzw. Wirklinien gezeichnet werden ist nicht vorgeschrieben, sie ist beliebig. Man könnte z.B. auch erst die Wirklinien von Fe und Ff zeichnen, so, dass sich sich schneiden und Ga irgendwie dazwischenfriemeln, oder erst die Wirklinie von Ff, dann irgendwo auf der Geraden den Anfang von Ga andocken lassen und mit der Wirklinie von Fe, die durch die Spitze von Ga verläuft vervollständigen, und und usw...
Teilsystem 2.
Teilsystem 1 erfolgreich gemeistert und um die Kenntnis des Betrags von Fe bereichert können wir uns zum Teilsysem 2 herüberschlingeln.
Das Vorgehen ist im Prinzip dasselbe wie oben. Wir kennen die Wirklinie, die Richtung und den Betrag von Fe. Hier, im Teilsystem 2 ist die Richtung von Fe entgegengestzt der Richtung im Teilsystem 1, denn wir betrachten ja jetzt Fe als die Kraft, die auf das Rohr B wirkt und diese Kraft hat nun einmal aus der Sicht von Rohr B :D genau die entgegengesetzte Richtung wie aus dem Blickwinkel von Rohr A betrachtet. Rohr A: "Rohr B drückt mit Fe von rechts unten!" Rohr B: "Rohr A drückt mit Fe von links oben!" Wegen actio gleich reaction ist der Betrag jedoch gleich und wir können endlich weiter machen. :-O
Wo waren wir doch noch gleich?! Ach ja! Die Beträge, Richtungen von Fe und Gb sind bekannt. Bekannt sind auch Richtungen und Wirklinien
von Fd, Fc. Von denen möchten wir aber auch die Beträge kennen. Die müssen wir sogar kennenlernen, sonst können wir das Teilsystem 3 nicht lösen. Intuitiv würde ich zuerst die Wirklinie von Fd zeichnen(sollte Deine Intuition nicht die meine sein, so macht das gar nichts, denn
die Zeichenreihenfolge ist ja bekanntlich beliebig. Hauptsache es kommt ein geschlossendes Krafteck zustande. :-))
Die horizontale Wirklinie von Fd ist nun fertig. Suchen wir uns einen Punkt auf Fd und lassen Gb betragsmäßig runterhängen. Dieser Punkt auf Fd kann der Anfang oder das Ende(die Spitze) von Fd sein, das ist Wurscht. Entscheiden wir uns doch einfach dafür, dass Gb an der Spitze von Fd andockt, das kommt der anfänglichen Vorstellung eines geschlossenen Krafteck vielleicht am nächsten und ich muss dann nicht mehr so viel blabla tippen. :-)
Nun haben wir wieder zwei Möglichkeiten, wir können von der Spitze von Gb aus die Wirklinie von Fc zeichnen und dann Fe, deren Richtung und Betrag wir kennen,irgendwie dazwischenfummeln, so, dass das Krafteck geschlossen ist. Ja, nicht jede Möglichkeit ist zugleich praktikabel. Versuchen wir stattdessen mal, vom Endpunkt der Kraft Gb die Kraft Fe mit Betrag und Richtung einzuzeichnen. Durch die Spitze
von Fe verläuft dann die Wirklinie von Fc und schneidet die Wirklinie von Fd und definiert damit zugleich diie Längen, also die Bätrage von Fd und Fc. Das war unser Ziel im System 2. Juhhuu! :-) Das sieht dann so aus:
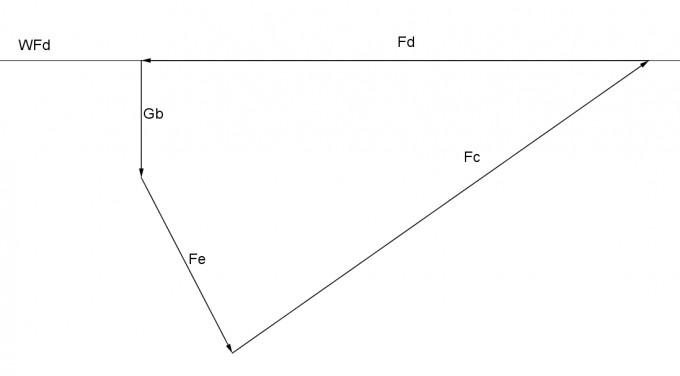
Aaaaaber das sieht doch ganz anders als in der Lösung aus! Querulant! Uuups stimmt! Messen wir doch mal nach: |Fd| ≈ 25.9 cm, |Fc| ≈ 26 cm. Ähhhh bitte was?! |Fd| ≈ 25.9 cm, |Fc| ≈ 26 cm ???? Maßstab von 10kN/cm ??? Also |Fd| = 25.9 cm * 10kN/cm = 260 kN und |Fc| = 26 cm * 10kN/cm = 260 kN ??? *In die Lösung guck* -> Stimmt! Na sowas, wieso? Ach jaaaa, die Reihenfolge der Vektoren im Krafteck ist ja Wurscht! *grins* Okay, vielleicht klappt es auch mit 100kN/cm einfach mal testen, ich habe eh geschummelt und das Krafteck per PC gezeichnet :O
Teilsystem 3.
Lösung verläuft prinzipiell wie die des Teilsystems 2. Bekannt: Gc, Fc, Wirklinien und Richtungen von Fa, Fb. Gesucht: |Fa|, |Fb|.
Ich möchte Dir nicht komplett die Freude am selbständigen Erarbeiten der Lösung der Aufgabe nehmen und wenn Du in meinem blabla eine Anregung bzw. Idee gefunden hast, diie Lösung zu vervollständigen, würde mich das freuen!
Beste Grüße
gorgar