Kolben eines Verbrennungsmotors. Wie kann ich den Hebelarm bestimmen?

Question

Hallo,

Also undzwar muss ich in der Aufgabe 5 (anhang) das Moment M bestimmen. Die Formel für M lautet ja M= F*a.  F ist ja schon gegeben aber wie bestimme ich den Hebelarm? 

(-> beste Antwort wird markiert wie immer :D )

MfG

Anhang:

Comments

EDIT: Wie kommt das Wort Hebelarm in die Überschrift? 

Bitte Text auch als Text eingeben: https://www.mathelounge.de/schreibregeln 

---

oh wollte eigentlich wie kann ich den Hebelarm bestimmen schreiben und nicht wie den Hebelarm bestimmen haha, da ich wissen wollte wie ich den Hebelarm bestimme/berechne habe ich das Wort in die Überschrift geschrieben

---

gelöscht da zwecklos

Answer 1

Hallo mistermathe,

den Hebelarm können wir uns selbst aussuchen, denn es ist ja nach dem Moment gefragt.
Nehmen wir doch einfach l₁ als Hebelarm. Dann ist das gesuchte Moment M = Fx · l₁.
Die Kraft Fx bekommen wir aus dem unteren Hilfsdreieck, die Hilfskraft Fh bekommen wir aus dem oberen Hilfsdreieck. Den Winkel beta bekommen wir mit dem Sinussatz. Wie man auf den Hilfswinkel alpha + beta kommt, habe ich in der Skizze eingezeichnet. Die bunten Winkel in der Skizze dienen dazu, damit Du die beiden Hilfsdreiecke in Deiner Aufgabenskizze wiedererkennst.

$$ M = F_x \cdot l_1 \\F_x = F_h \cdot \sin(\alpha + \beta) \\F_h = \frac{F}{\cos(\beta)} \\\sin(\beta) = \frac{l_1}{l_2} \sin(\alpha) \Rightarrow \beta = \arcsin \left (\frac{l_1}{l_2} \sin(\alpha)  \right )\\$$

Damit haben wir die benötigten Formeln. Jetzt werden nur noch \( F_x, F_h, \) und \( \beta \) nacheinander in die Momentengleichung \( M = F_x \cdot l_1 \) eingestetzt.

$$M = F_h \cdot \sin(\alpha + \beta) \cdot l_1 = \frac{F}{\cos(\beta)}\cdot \sin(\alpha + \beta)\cdot l_1 = \\ F \cdot \frac{\sin\left (\alpha +  \arcsin \left (\frac{l_1}{l_2} \sin(\alpha)  \right )  \right )}{\cos\left ( \arcsin \left (\frac{l_1}{l_2} \sin(\alpha)  \right ) \right )}\cdot l_1\\ $$

Wenn M in der Aufgabenskizze das gesuchte Moment ist, dann ist es definitionsgemäß positiv, weil es linksdrehend ist. Warum in Deiner Lösungshilfe ein Minuszeichen davor steht, verstehe ich gerade mal nicht.

Beste Grüße
gorgar

Comments

Hallo gorgar,

Du schreibst: "Warum in Deiner Lösungshilfe ein Minuszeichen davor steht, verstehe ich gerade mal nicht."

Das \(F_X\) hat die falsche Orientierung. Daher dreht Dein Moment nach links, korrekt wäre aber rechts herum.

Gruß Werner

---

Hallo Werner,

in der Aufgabe dreht doch das gesuchte Moment auch nach links.

Gruß
gorgar

---

Hmm ? - stimmt. Was bedeutet: "steht im Gleichgewicht"? Ich hatte die Aufgabe so verstanden, das Moment zu suchen, welches die Pleuelstange auf den Punkt \(A\) ausübt. Und den roten Pfeil hatte ich als positive Richtung interpretiert.

Aber Du hast Recht - im Gleichgewicht ist das links drehende - also positive Moment.

Gruß Werner

---

Okay, ich habe das mit dem "im Gleichgewicht stehend" so interpretiert:

Die Kraft F drückt von oben den Kolben runter. Das bewirkt eine Rechtsdrehung der Komponente l1, also ein rechtsdrehendes, negatives Moment. Fx wirkt der von oben drückenden Komponente von F  entgegen. Das für "Gleichgewicht" sorgende Gegenmoment wäre demnach linksdrehend und positiv, so wie in der Aufgabe skizziert.

Beste Grüße
gorgar

---

Woher weiß man ob M linksdrehend oder rechtsdrehend ist ?

---

Meinst Du jetzt das \(M\) welches hier gesucht ist oder ist die Frage allgemeiner Natur - also woran man bei einem Moment allgemein die Richtung erkennt?

 

Am einfachsten aus der Anschauung. Diese Kraft \(F\) mit dem Hebel \(a\) bewirkt ein links drehendes - also positives Moment - um den Punkt \(A\).

Rein formal aus dem Vektorprodukt. In der obigen Aufgabe ist der Hebel in vektorieller Darstellung

$$\vec{a} = l_1 \begin{pmatrix} \sin(\alpha) \\ \cos(\alpha) \end{pmatrix}$$

und der Kraftvektor der Kraft, die von der Pleuelstange auf den Hebel ausgeübt ist, ist

$$\vec{F_P} = F_P \begin{pmatrix} \sin(\beta) \\ -\cos(\beta) \end{pmatrix}$$

Das Moment \(M_P\), das \(F_P\) auf \(A\) ausübt, ist dann

$$M_P= \vec{a} \times \vec{F_P} = l_1 \begin{pmatrix} \sin(\alpha) \\ \cos(\alpha) \end{pmatrix} \times F_P \begin{pmatrix} \sin(\beta) \\ -\cos(\beta) \end{pmatrix}$$

$$\space = l_1 \cdot F_P \cdot \left(  -\sin(\alpha) \cos(\beta) - \cos(\alpha)\sin(\beta) \right) = - l_1 \cdot F_P \cdot \sin(\alpha + \beta)$$

ist also bei den kleinen Winkeln in jedem Fall negativ - also rechtsdrehend. Das Gegenmoment - also das Moment was mit \(M_P\) im Gleichgewicht steht - muss natürlich anders herum drehen, bzw. hier ein positives Vorzeichen haben, da sich beide Momente aufheben müssen, um im Gleichgewicht zu stehen.

---

Woher weiß man ob M linksdrehend oder rechtsdrehend ist ?

Indem Du auf die Zeichnung der Aufgabenstellung guckst und feststellst, dass das gesuchte, rot eingezeichnete Moment  M links herum, gegen den Uhrzeigersinn,  also in die mathematisch positiv definierte Richtung dreht, wobei auch Drehmomente in dieser Richtung positiv gewertet werden. :O

Auch ohne das rot eingezeichnete M kannst Du Dir überlegen, dass die Kraft F die Kurbelwelle bzw. das Bautel l₁ rechts herum drehen lässt und daher ein negativ gewertetes Moment zur Folge hat und deshalb das gesuchte Gegenmoment entgegengesetzt wirken und positiv sein muss.

Viele Grüße
gorgar

Answer 2

Hallo mistermathe,

Wichtig ist - wie so oft - das man sich alles noch mal aufzeichnet und sich klar macht, was gegeben ist und welche Größen gesucht sind.

Die Gleichung \(M=a \cdot F\) gilt genau nur dann in der Form, wenn \(a\) und \(F\) skalarer Natur sind und und \(a\) senkrecht auf \(F\) steht. Oder eben, wenn \(a\) und \(F\) als Vektoren gegeben sind - dann lässt sich das Moment aus dem Kreuzprodukt der bedien Größen berechnen und dann müssen beide Größen auch nicht senkrecht auf einander stehen.

Ich mache es hier ohne Vektoren - dann ist der Abstand \(a\) der Wirkungslinie der Kraft vom Drehpunkt \(A\) gesucht.

 

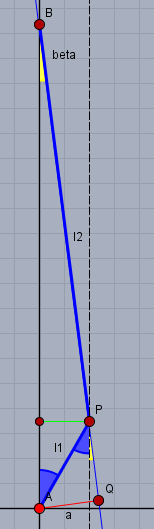
Oben siehst Du die Strecke und damit den Hebelarm \(a\) (rot) eingezeichnet. Der gelbe Winkel sei \(\beta\). Eine wesentliche Erleichterung bei der Lösung dieser Aufgabe besteht darin, das Dreieck \(AQP\) zu 'sehen'. Hier gilt nämlich

$$\sin{(\alpha + \beta)} = \frac{a}{l_1}$$

Der Winkel \(\beta\) lässt sich über die grün eingezeichnete Strecke \(e\) berechnen. Aus \(e = l_1 \cdot \sin(\alpha)\) und \(e=l_2 \cdot \sin(\beta)\) folgt

$$\sin(\beta) = \frac{l_1}{l2} \sin(\alpha)$$

und damit lässt sich \(a\) bereits hinschreiben

$$a = l_1 \cdot \sin{\left( \alpha + \arcsin\left( \frac{l_1}{l2} \sin(\alpha)\right) \right)}$$

Deine Annahme, dass \(F\) (für das Moment) bereits gegeben ist, ist falsch. Da das Lager der Pleuelstange reibungsfrei ist, wirkt die Kraft in der Stange nur in Richtung der beiden Aufhängepunkte der Stange. Die gegebene Kraft \(F\) teilt sich in eine Kraft senkrecht zum Hub und in die Kraft \(F_P\), die in Richtung der Pleuelstange.

 

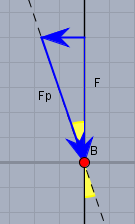
Der gelbe Winkel ist wieder \(\beta\) (s.o.). \(F_P\) berechnen sich aus

$$F_P=\frac{F}{\cos( \beta )}$$

Das gesuchte Moment ist \(M=-a \cdot F_P\). Das Minuszeichen resultiert aus der Vorgabe, dass ein positives Moment links drehend sein soll und so wie ich oben die Größen definiert habe, ist das Moment aber rechts drehend - daher das Minus. Jetzt haben wir alle Größen bestimmt und brauchen nur noch einsetzen:

$$M=-  l_1 \cdot \sin{\left( \alpha + \arcsin\left( \frac{l_1}{l2} \sin(\alpha)\right) \right)} \cdot \frac{F}{\cos \left( \arcsin \left( \frac{l_1}{l2} \sin(\alpha)\right) \right)}$$

$$\space =- l_1 \cdot F \cdot \frac{\sin{\left( \alpha + \arcsin\left( \frac{l_1}{l2} \sin(\alpha)\right) \right)}}{\cos \left( \arcsin \left( \frac{l_1}{l2} \sin(\alpha)\right) \right)}$$

Gruß Werner