Hallo Leute
bräuchte Hilfe bei folgender Aufgabe.
Aufgabe:
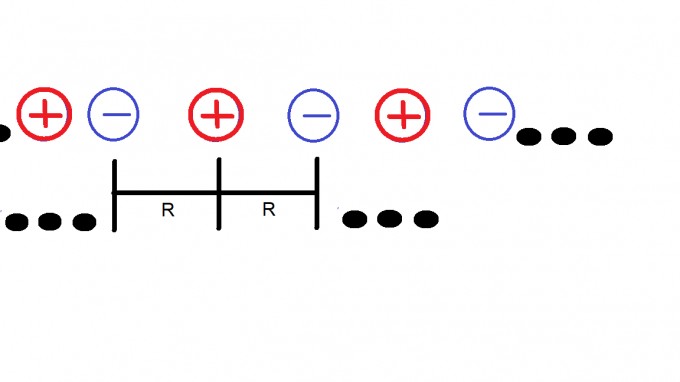
Betrachten Sie eine mit der positiven Ladung Q geladene Punktladung die zunächst zwei negative Punktladungen ( jeweils -Q) als nächste Nachbarn entlang einer eindimensionalen Linie hat. Der Abstand zwischen zwei nächsten Nachbarn betrage immer R.
a.) Berechnen Sie die elektrostatische Energie der positiven Ladung.

b.) Betrachten Sie nun die unendlich ausgedehnte eindimensionale Kette aus Punktladungen abwechselnder Polarität.
Berechnen Sie wieder die elektrostatische Energie der positiven Punktladung.
Anmerkung : die dreidimensionale Version dieser Aufgabe ist ein übliches Modell für die Bindungsenergie von ionischen Kristallen wie z.B. Kochsalz(NaCl).
Problem/Ansatz:
Leider komme ich mit der Aufgabe überhaupt nicht zurecht.
Im Skript ahben wir :
W = Arbeit, die man am System verrichtem muss, um eine Ladungskonfiguration zuverändern.
W2 = q1 * q2 / ( 4* π * ε0 * ) * (1/r2 - 1/r1 )
Definition :
Die elektrostatische Energie U einer Ladungskonfiguration ist diejenige Arbeit, die man verrichten muss, um diese Konfiguration aus ∞ großen Abständen der Ladungen aufzubauen.
Allerdings habe ich zu U keinerlei Formel.
Ist U das elektrische Potential ? Ich habe hier echt komplett den Überblick verloren.
Und vor allem wie soll ich ohne Werte rechnen ? Habe ja kein R oder q. Will der Aufgabensteller dass wir die Formel zur Berechnung von U raus finden ?
Liebe Grüße Kevin
