Hallo,
hier die Lösung:
Zunächst zu deiner Frage bezüglich der Phasendrehung durch die Leitung l2:
Das Winkelmaß ist angegeben mit \(\small βl = 23^{o}\). Rechnet man das Winkelmaß um in Teil der Wellenlänge, so erhält man
\(\small βl = 0,06388*λ = 0,4792m\)
(Da f = 40 MHz , beträgt \(\small λ = 7,5m\))
Damit lässt sich Frage 1 beantworten: l1 = 1,875m und l2 = 0,4792m
Zur Frage 2: Da die Leitungsimpedanz Z0 = 60 Ohm beträgt, wird auch die Bezugsimpedanz mit 60 Ohm festgelegt. Auf diesen Wert werden auch die Impedanzen Z1 bis Z6 normiert.
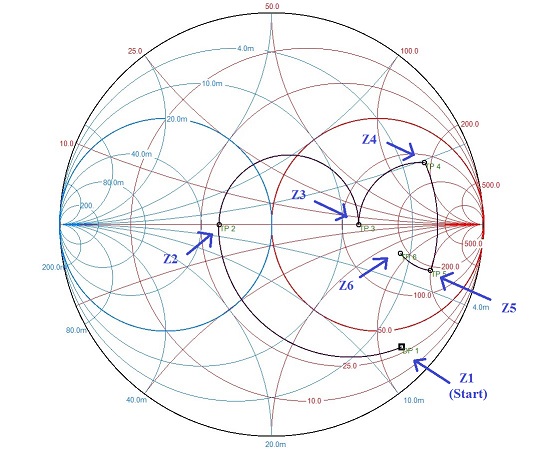
Zur Frage 3: Mit den angegebenen Impedanzwerten des Netzwerks und dem bereits ermittelten Winkelmaß l2 können jetzt die Impedanzen Z1 bis Z6 mit Hilfe des Smithdiagramms ermittelt werden. Als Ergebnis erhält man (siehe Smithdiagramm Bild 1):
\(\small \underline Z_{1} = (30 - j120)Ω \text{ normiert auf 60Ω : } 0,5 - j2\)
\(\small \underline Z_{2} = (30 - j0)Ω \text{ normiert auf 60Ω : } 0,5 - j0\)
\(\small \underline Z_{3} = (120 - j0)Ω \text{ normiert auf 60Ω : } 2 - j0\)
\(\small \underline Z_{4} = (120 + j180)Ω \text{ normiert auf 60Ω : } 2 + j3\)
\(\small \underline Z_{5} = (198 - j180)Ω \text{ normiert auf 60Ω : } 3,3 - j3\)
\(\small \underline Z_{6} = (186 - j180)Ω \text{ normiert auf 60Ω : } 3,1 - j3\)
Bild 1:
Zur Frage 4:
Das VSWR lässt sich über den Betrag des komplexen Reflexionsfaktor \(\small \vert\underline r\vert\) nach folgender Gleichung berechnen:
\(\small VSWR = \frac{1 + \vert\underline r\vert}{1 - \vert\underline r\vert}\)
wobei sich der komplexe Reflexionsfaktor \(\small \underline r\) nach folgender Gleichung berechnet
\(\small \underline r = \frac{\underline Z_{L} - \underline Z_{0}}{\underline Z_{L} + \underline Z_{0}}\)
mit \(\small \underline Z_{L} = Lastwiderstand\) und \(\small \underline Z_{0} = Wellenwiderstand\).
Als Ergebnis erhält man für das VSWR am Leitungseingang = 3,605
VSWR an der Last = 10,402
Gruß von hightech