Hallo Daniel,
Empfehlung: Skizze:
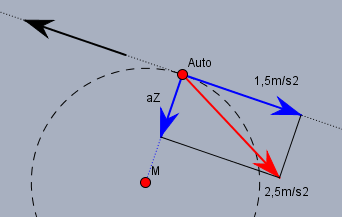
dort siehst Du die momentane Fahrtrichtung des Autos, sowie die maximal zulässigen Beschleunigungen als blaue und rote Pfeile. Die maximale Beschleunigung, die das Auto über die Räder erfahren kann ist auf Grund der Nässe \(a_{\text{max}}=\mu \cdot g=2,5 \text{m}/\text{s}^2\).
Es ist eine Bremsbeschleuingung von \(1,5\text{m}/\text{s}^2\) gefordert (der blaue Pfeil, der gegen die Fahrtrichtung zeigt). Die Gesamtbeschleunigung setzt sich aus der Bremsbeschleunig und der Zentripetalbeschleunigung \(a_z\) zusammen, die das Auto auf Spur hält (blauer Pfeil in Richtung des Kreismittelpunkts). Beide stehen senkrecht auf einander, so lässt sich die maximal mögliche Zentripetalbeschleunigung nach Pythagoras berechnen:
$$a_Z=\sqrt{2,5^2-1,5^2}\frac{\text{m}}{\text{s}^2} = 2\frac{\text{m}}{\text{s}^2}$$
Für die Zentripetalbeschleunigung gilt \(a_Z=v^2/r\). Mit gegebenem Radius \(r=24,5\text{m}\) erhält man
$$v=\sqrt{a_Z \cdot r} = \sqrt{ 2\frac{\text{m}}{\text{s}^2} \cdot 24,5\text{m} } = 7 \frac{\text{m}}{\text{s}}=25,2 \frac{\text{km}}{\text{h}}$$