Hallo Leute,
ich stehe vor einer Aufgabe. Undzwar soll ich folgende T und Pi Schaltungen als Lineares Gleichungssystem aufschreiben. Das Thema kommt aus der Zweitortheorie. Die Aufgabe lautet wie folgt:
Beschreiben Sie die beiden nachstehenden Netzwerke durch Gleichungen der Gestalt:
$${U}_{e} = {a}_{1,1} + {U}_{a} + {a}_{1,2}\cdot{I}_{a}$$
$${I}_{e} = {a}_{2,1} + {U}_{a} + {a}_{2,2}\cdot{I}_{a}$$
$$\Leftrightarrow$$
$$\begin{pmatrix}{U}_{e}\\{I}_{e}\end{pmatrix} = \underbrace{\begin{pmatrix} {a}_{1,1} & {a}_{1,2} \\ {a}_{2,1} & {a}_{2,2} \end{pmatrix}}_{\rm =:A}\cdot \begin{pmatrix} {U}_{a}\\{I}_{a}\end{pmatrix}$$
Und geben Sie jeweils die zugehörige Kettenmatrix A an !
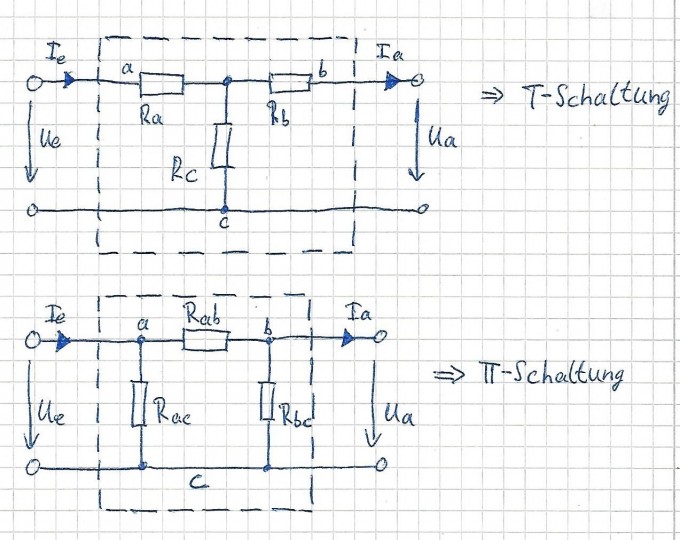
Begründen Sie, wie sich die Widerstände der einen Schaltung in die der anderen so umrechnen lassen, dass sich beide Netzwerke bezüglich ihrer äußeren Anschlüsse "vollkommen identisch" verhalten.
Bis hierhin geht die Aufgabe:
Ich weiss, das ich mittels der T und Pi Schaltungen ein Lineares Gleichungssystem, die der Gestalt wie oberhalb der Schaltungen angegeben, bestimmen muss. Halt einmal als Gleichung und anschließend als Vektor Schreibweise. Nur wie komme ich darauf ? Wie bestimme ich die Kettenmatrix A ?
VG :)