Hallo,
bei dieser Schaltung handelt es sich um einen Tiefpass, bei dem der Amplitudengang und Phasengang gesucht sind.
Resonanz oder Resonanzfrequenz gibt es hier nicht! Der Index 0 bei ω0 steht für Grenzfrequenz, die unten berechnet wird.
Auf den Tiefpass lässt sich die Spannungsteilerregel anwenden:$$\underline U_{C} = \underline U * \frac{\frac{1}{jωC}}{R + \frac{1}{jωC}}$$
Durch Umstellen erhält man die komplexe Übertragungsfunktion:$$\underline A = \frac{\underline U_{C}}{\underline U} = \frac{1}{1+jωRC}$$
und daraus den Betrag der komplexen Übertragungsfunktion \(\vert\underline A\vert\)
$$\vert\underline A\vert\ = \frac{U_{C}}{U} = \frac{1}{\sqrt{1+(ωRC)^{2}}}$$
Den Amplitudengang zeigt Bild 1
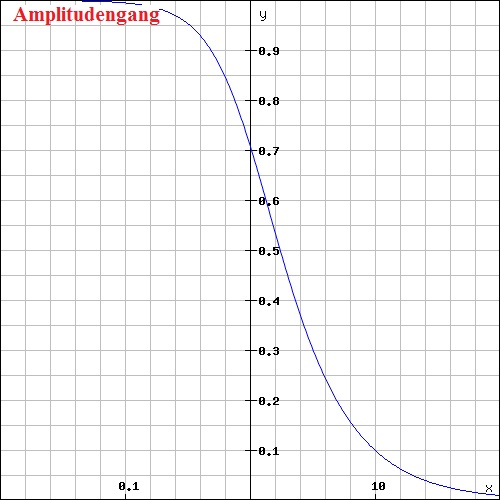
Von besonderem Interesse ist die Frequenz, bei der R und 1/jωC gleich groß sind und wie groß bei dieser Frequenz der Betrag der komplexen Übertragungsfunktion ist. Zur Kennzeichnung erhält diese Frequenz, die so genannte Grenzfrequenz, den Index 0. Durch Gleichsetzen erhält man \(R = \frac{1}{jω_{0}C}\)
aufgelöst nach der Frequenz \(ω_{0} = \frac{1}{RC}\text{ bzw. } f_{0} = \frac{1}{2πRC}\)
Setzt man ω0 in die Übertragungsfunktion ein, also für R•C den Wert \(\frac{1}{ω_{0}}\), erhält man$$\vert\underline A\vert\ = \frac{U_{C}}{U} = \frac{1}{\sqrt{1+(\frac{ω}{ω_{0}})^{2}}}$$
Für \(ω = ω_{0}\text{ wird } \frac{U_{C}}{U} = \frac{1}{\sqrt{1+1}} = \frac{1}{\sqrt{2}}\)
Der Phasengang der komplexen Übertragungsfunktion ergibt sich zu $$φ(\underline A )= φ{Z} - φ{N} = 0^{0} - arctan(\frac{\text{ Im(Nenner) }}{Re(Nenner)})$$
Den Phasengang zeigt Bild 2
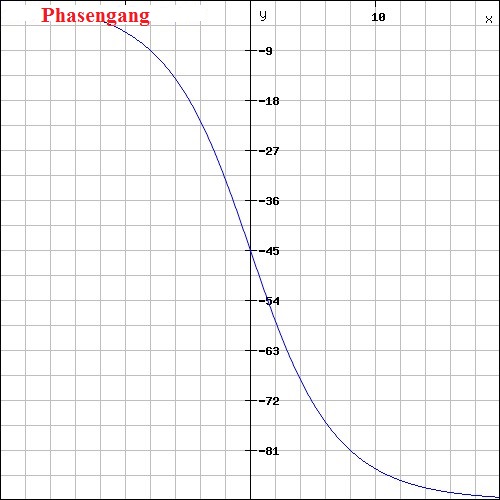
Gruß von hightech