Ortskurve Z=f(w/wo) für Schaltung zeichnen bei wo=1/(RC)

Question

Hallo,

ich soll zu folgender Aufgabe eine Ortskurve zeichnen:

muss ich hier selbst Frequenzen wählen? Wie fange ich an?

Comments

ich würde ja gern behilflich sein und habe auch versucht mich
über das Internet schlau zu machen, habe aber dort nichts
gefunden.
Rein mathematisch kann ich mit den Angaben kaum etwas
anfangen.
mfg Georg

---

Das ist gerade mein Problem ;)

---

  Du mußt doch Fachmann sein um die Frage zu verstehen.

  Unter http://de.wikipedia.org/wiki/Blindwiderstand 

ist bei Blindwiderstand / Kondensator  schon einmal etwas
ähnliches angeführt.

---

Es sind doch sieben Werte (inklusive unendlich) für die Frequenzen angeben (skaliert auf die Resonanzfrequenz).

---

"ich würde ja gern behilflich sein und habe auch versucht mich
über das Internet schlau zu machen, habe aber dort nichts
gefunden.
Rein mathematisch kann ich mit den Angaben kaum etwas
anfangen.
mfg Georg"

Dazu braucht man weder Wikipedia noch sonstwas aus dem Internet. Das ist Inhalt der Vorlesung "Grundlagen der E-Technik" erstes Semester. Das einzige was man dazu braucht ist die komplexe Rechnung.

"Es sind doch sieben Werte (inklusive unendlich) für die Frequenzen angeben (skaliert auf die Resonanzfrequenz)."

Resonanzfrequenz ??? Hier gibt es keine Resonanzfrequenz!

Gruß von hightec

Answer 1

Hallo,

hier die Lösung:

Der Komplexe Widerstand Z berechnet sich aus der Parallelschaltung von R und C$$\underline Z = \frac{R*\frac{1}{jωC}}{R + \frac{1}{jωC}}$$

bzw.$$\underline Z = \frac{R}{1 + jωRC}$$

setzt man für R*C die Grenzfrequenz 1/ω₀ ein hält man$$\underline Z = \frac{R}{1 + j*\frac{ω}{ω_{0}}}$$

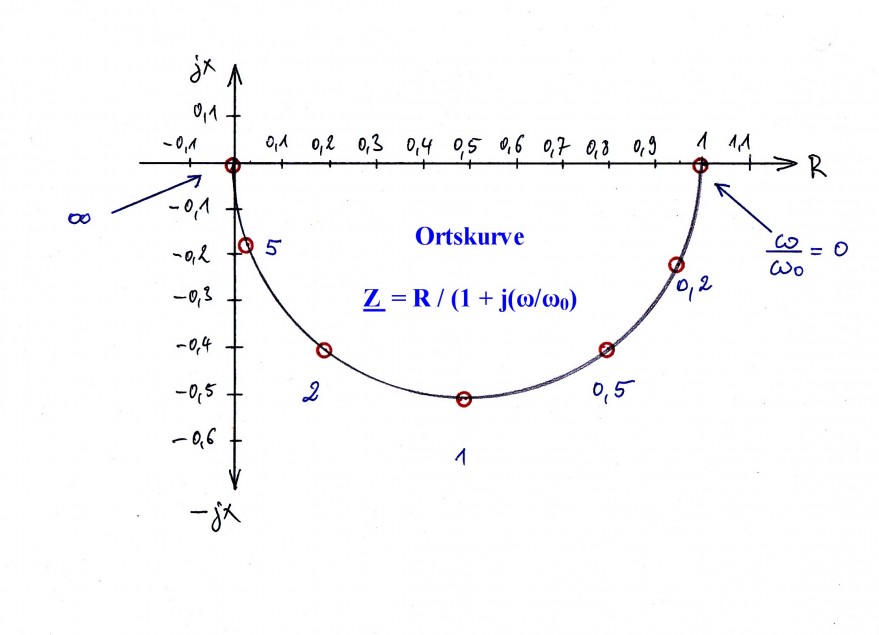
Diese Gleichung mit der normierten Variablen ω/ω₀ stellt in der komplexen Ebene ein nach oben geöffneter Halbkreis dar, siehe Bild.

Hier die berechneten Werte:

ω/ω₀     0                 0,2                   0,5                 1              2                      5                 ∞

Z       R + j0    0,962 - j0,192    0,800 - j400    0,5 - j0,5    0,2 - j0,4    0,0385 - j0,192  0 - j0

Die gesuchten Werte sind eingetragen.

Gruß von hightech