Welche Spannung ist bei Ux zu erwarten?

Question

+Ub ist 15 V

-Ub ist -15 V

Die Frage ist, welche Spannung ist bei unterem sowie Oberem Ausschlag zu erwarten.

ich habe eine Antwort erhalten .

Diese besagt die Spannung bei Ux liegt zwischen + 1,36 und - 1,36 Volt.

Leider kann ich das nicht nachvollziehen-

Vor alles wenn Rx --> 0 Ohm ist..dann fällt da doch gar keine Spannung ab.

Answer 1

Hallo, hier die Lösung:

Die Aufgabe wird mit Hilfe des "Überlagerungssatzes" gelöst. Nach diesem Prinzip wird zunächst die Spannung - U_b zu Null gemacht und dann die Spannung U+ berechnet (siehe Skizze) wenn also nur die positive Spannung + U_b vorhanden ist. Anschießend wird die Spannung + U_b zu Null gemacht und ebenfalls U_x berechnet, wenn nur die negative Spannung - U_b vorhanden ist. Anschließend werden die Spannungen U_x aus beiden Berechnungen addiert. Das Ergebnis ist dann die Spannung, wenn das Potentiometer am linken Anschlag steht. Das gleiche Verfahren wird angewandt um die Spannung bei Rechtsanschlag des Potis zu berechnen. Wichtig: die gesuchte Spannung Ux liegt dann allerdings an der rechten Seite des Potis an.

Noch ein Hinweis: Eine Spannung "zu Null machen" bedeutet sie zu überbrücken, d.h. kurzzuschließen. Es leuchtet ein, dass dann der positive Anschluß der Spannungsquelle ebenfalls auf Masse liegt bzw. der negative Anschluß von - U_b wenn - U_b überbrückt wird. Damit ist auch klar, weshalb der 1K und der 10K Widerstand parallel geschaltet sind.

 

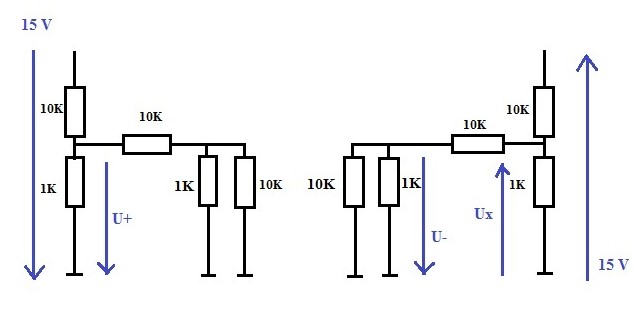
Hier die Berechnung:

- U_b = 0

U+ = 12V • {[(1K||10K) + 10K] || 1K} / {{[(1K||10K] + 10K) || 1K} + 10K}

den Zähler ausgerechnet ergibt Z = 0,91603 KOhm

den Nenner ausgerechnet ergibt 10,91603 KOhm

U₊ = 12V • 0,91603 KOhm / 10,91603 KOhm

U₊ = 1,2587 V

+ U_b = 0

Hier beachten, dass U- (anders als U+) an einem weiteren Spannungsteiler liegt!!!

U- = U_x • (1K||10K) / [(1K||10K) + 10K]

da die Berechnung für U_x  identisch ist mit der Berechnung für den U+ aus obiger Rechnung (siehe - U_b), kann darauf verzichtet werden.

U_x = 1,2587 V

U- = U_x •  (1K||10K) / [(1K||10K) + 10K]  = 1,2587V • 0,916KOhm /10,916KOhm

U- = 0,1056 V

Die Spannung auf der linken Seite des Potis ist somit  U = U₊ + U_-  = 1,2587 V + 0,1056 V  = 1,364 V

Das gleiche Ergebnis erhält man bei Berechnung auf der rechten Seite des Potis.