Arbeit, die die Schwerkraft verrichtet hat , wenn das Seil zum ersten Mal durch die Vertikale schwingt

Question

Eine Masse von 4.90 kg hängt an einem Seil der Länge 0.42 m, das an einem Haken in der Decke befestigt ist. Die Masse befindet sich zunächst ruhend in einer Position, bei der das Seil mit der Vertikalen einen Winkel von θ = 45° einschließt, und wird dann losgelassen.
Berechnen Sie die Arbeit, die die Schwerkraft verrichtet hat, wenn das Seil zum ersten Mal durch die Vertikale schwing

Answer 1

Die Arbeit im Schwerefeld ist definiert als Differenz der potentiellen Energie.

Es wird nur Arbeit verrichtet, wenn der Körper gegen die Schwerebeschleunigung bewegt wird, horizontale Bewegungen erfordern keine Arbeit.

Bezeichnet man also die vertikale Achse mit x, dann gilt für die verrichtete Arbeit:

ΔW = m*g*Δx

Nun ein kleines Bild zur Aufgabe:

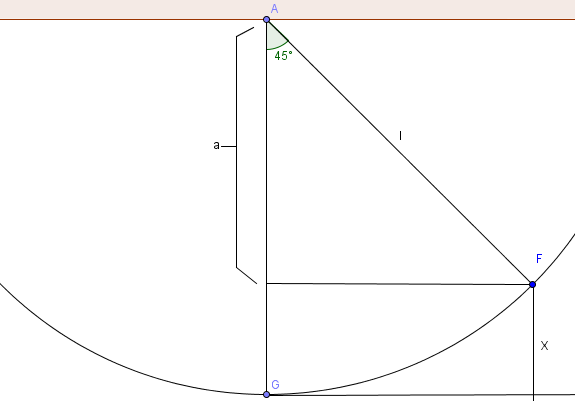
Die Größe die wir suchen ist im Bild mit X bezeichnet.

Man sieht leicht, dass daher

Δx = l - a

gilt.
Außerdem bilden a und l ein rechtwinkliges Dreieck, in dem gilt:

cos (θ) = a/l

Also: a = l*cos(θ)

Damit folgt:
Δx = l*(1-cos(θ))

Also

ΔW = mgl*(1-cos(θ))

Setzt man nun ein
m = 4.9 kg

g = 9.81 m/s²

l = 0.42 m

θ = 45°

 

dann erhält man:

ΔW ≈ 5.913 J