Kräfteplan. Berechne die Seilkraft

Question

 Ich habe hier folgende Aufgabe zu lösen:

 

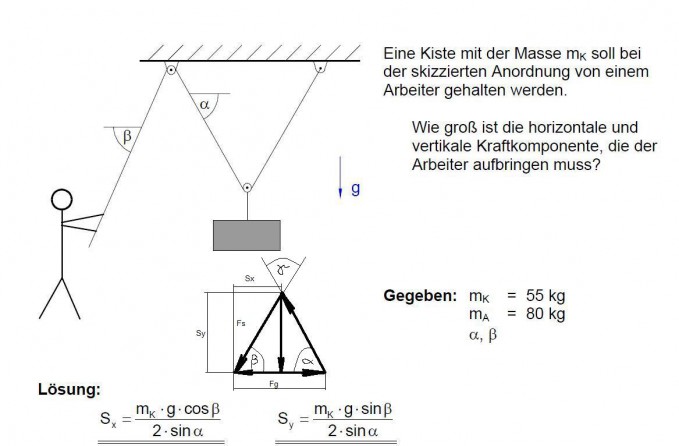
Der Kräfteplan ist von mir selbst angelegt, schien mir am einfachsten den in Paint eben mit rein zu zeichnen ;)

Hier bin ich folgendermaßen vorgegangen:

Sinussatz:
$$\frac{m \cdot g}{sin (γ)}=\frac{F_s}{sin(α)} ⇒ F_s=\frac{m \cdot g \cdot sin(α)}{sin(γ)}$$

$$Kraftkomponentenzerlegung:$$

$$S_x= sin(β) \cdot F_s$$

$$S_y= cos(β) \cdot F_s$$

$$Einsetzen   von F_s$$

$$S_x= \frac{sin(β) \cdot m \cdot g \cdot sin(α)}{sin(γ)}$$

$$S_y= \frac{cos(β) \cdot m \cdot g \cdot sin(α)}{sin(γ)}$$

ich habe hier nicht das gleiche Ergebnis wie in den Lösungen angegeben aber ich müsste doch eigentlich auch richtig liegen oder habe ich etwas übersehen? danke im voraus ;)
mfg, Subis

Comments

es soll überall anstatt

$$m$$
 $$m_k$$ heißen

Answer 1

ich habe lange überlegen müssen ( allerdings keine 5 Tage am Stück )

Bild 1 zeigt die Kraft  die in beiden Seilen auftritt ( F1 ).
Es wird so getan als ob oben links keine Umlenkrolle ist.

Bild 2 zeigt das Kräfteparallelogramm

Bild 3 zeigt den oberen Teil des Kräfteparallelogramms
Es ergibt sich sin ( alpha ) = ( F/2 ) / F1
F1 = F / ( 2 * sin ( alpha ))

Diese Kraft F1 wirkt nun über die Umlenkrolle auch im Seil auf der
linken Seite. ( Habe ich nicht gut gezeichnet. F1 links und F1 rechts
müssen die gleiche Länge haben ).

Bild 4.)
sin ( beta ) = sy / F1
sy = sin ( beta  ) * F1 =
sy = sin ( beta ) * F /  ( 2 * sin ( alpha ))

cos ( beta ) = sx / F1
sx = cos ( beta  ) * F1
sx = cos ( beta ) * F /  ( 2 * sin ( alpha ))

Answer 2

$$ F_S= \frac{m \cdot g}{\sin \alpha} $$

täte es wohl auch und ergibt weniger Rundungsfehler, wenn man versucht das unter Wiederverwendung gerundeter Zwischenergebnisse mit dem TR zu bewältigen.

Comments

Wie kommst du denn auf diesen ansatz? Hab auch schon überlegt ob das geht aber normalerweise wäre es doch nur mg/2 oder nicht?

Das seil hat ja sozusagen 2 feste lager einmal rechts im bild und links die person die "zieht" und hier muss die kraft sich doch aufteilen oder sehr ich das falsch?

wäre dann ja sogar Fs=mg/2sin(α)

---

Kräfteparallelogramm:

KräfteparallelogrammSymmetrisch.ggb (10 kb)

---

ich kenne das Kräfteparallelogramm habe absichtlich im plan oben nur das halbe gezeichnet^^

ich meinte aber, dass die kraft sich aufteilen muss da es in zwei entgegengesetzten Richtungen gelagert ist (sorry wenn ich es grad so schlecht beschreiben kann was ich meine)

kann mir sonst nicht erklären wieso in der Lösung im Nenner 2sin(α) steht

trotzdem schonmal danke für deine mühe ;)

---

habe nun folgenden lösungsweg erarbeitet:

$$F_s=\frac{m_k \cdot g}{2 \cdot sin(α)}$$ diesen Ansatz gewählt, da die kraft am seil aufgeteilt wird aufgrund von 2 Festlagern.

$$F_{s_y}=F_s \cdot sin(β)=\frac{m_k \cdot g \cdot sin(β)}{2\cdot sin(α)}$$

$$F_{s_x}=F_s \cdot cos(β)=\frac{m_k \cdot g \cdot cos(β)}{2\cdot sin(α)}$$

---

Ich konnte Deinem Erstansatz nicht wirklich folgen und dachte, wir fangen mal kleinschrittig an mit der Seilkraft ohne Komponentenzerlegung.

Bedauerlicherweise habe ich dabei geschlampt und das Halbieren vergessen.

Jetzt sieht Deine Lösung nachvollziehbar und richtig aus.

---

Ja das war wohl käse, hab erst versucht alles als ein einzelnes system zu betrachten aber daa hat nicht witklich geklappt :D

Ist ja auch nur eine kleinigkeit mit dem halbieren aber es hat mir auf jeden fall zur lösung verholfen denk ich.

Vielen dank,

lg subis