Hallo xxx,
eine Skizze zum Problem:
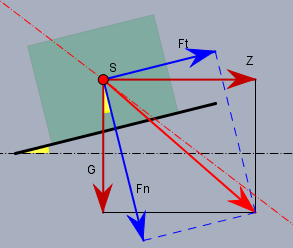
Gewichtskraft \(G\) und Zentrifugalkraft \(Z\) addieren sich zu der hellroten Gesamtkraft. Diese wiederum teilt sich auf in die Normalkraft \(F_N\) senkrecht zur schiefen Ebene und der Tangentialkraft \(F_T\) parallel zur Ebene (beide blau). Die Reibung hält die Masse genau dann ausreichend fest, wenn \(F_T \div F_N \le 0,8\) ist. Heißt formal
$$\arctan \frac{Z}{G} - \alpha \le \arctan 0,8$$
Wobei \(\alpha\) (gelb) der Winkel der Ebene gegenüber der Horizontalen ist. Mit \(G=m \cdot g\) und \(Z=m \cdot v^2/r\) und dem Additionstheorem von \(\tan(\alpha + \beta)\) erhält man:
$$v \le \sqrt{ r \cdot g \cdot \tan( \arctan 0,8 + \alpha ) } = \sqrt{30 \cdot 9,81 \cdot \frac{0,8 + 0,15}{1 - 0,8 \cdot 0,15} } \frac{\text{m}}{\text{s}} \\ \space \approx 17,8 \frac{\text{m}}{\text{s}} \approx64,2 \frac{\text{km}}{\text{h}}$$
Nachtrag nach Hinweis von hj2166 (s.u.): und wenn man statt 15% Steigung die angegebenen 5% einsetzt, erhält man
$$v \le \sqrt{30 \cdot 9,81 \cdot \frac{0,8 + 0,05}{1 - 0,8 \cdot 0,05} } \frac{\text{m}}{\text{s}} \approx 58,1 \frac{\text{km}}{\text{h}}$$ Gruß Werner