Hallo Helin,
Das Prinzip der virtuellen Arbeit besteht darin, bei der interessierenden Kraft das 'festhaltende' Lager durch eine Kraft zu ersetzen. Anschließend wird angenommen, dass sich das System um eine virtuelle Betrag verschiebt und die Summe der dabei anfallenden Arbeit wird zu 0 gesetzt. In diesem Fall mache ich aus dem Lager \(A\) ein Loslager, welches sich in \(X\) verschieben lässt und ersetzte es durch eine Kraft \(A_x\).
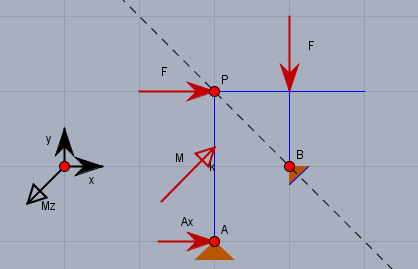
Das ganze System kann nun um den Pol \(P\) um \(\text{d}\varphi\) gedreht werden. Ich nehme die Drehung linksdrehend als positiv. Die Summe der virtuellen Arbeiten ist $$2aA_x \text{d}\varphi - M \text{d}\varphi - aF \text{d}\varphi = 0$$ Die Kraft, die in \(P\) angreift, hat keinen Einfluss auf die Drehung um \(P\). Mit \(M=aF\) ist dann $$A_x= F $$ Gruß Werner