Hallo probe,
Eine Bemerkung im Vorfeld. Dir ist das klar was die einzelnen Buchstaben bedeuten, aber ich wusste zunächst nicht, was Du mit \(E\) und \(I\) oder \(EIw\)(?) meinst. Es war auch überhaupt nicht klar, wie Du auf \(C_1=-qL/2\) kommst. Hätte ich das gleich gewusst, hätte ich Dir gestern Abend bereits helfen können. Es wäre hilfreich, wenn Du von vornherein beschreibst, was die einzelnen Größen bedeuten und wo die Gleichungen herkommen.
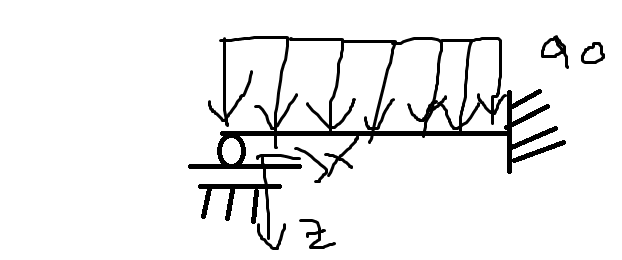
Deinen Ansatz finde ich ok, Voraussetzung ist, dass die konstante Streckenlast \(q\) wirklich über den gesamten Bereich läuft, aber das ist ja gegeben (s. https://www.nanolounge.de/13670/krafte-bestimmen-2-beispiele-mit-streckenlast).
Aus \(w(x=0)=0\) folgt unmittelbar \(C_1=0\). Aus \(w''(x=0)=0\) folgt \(C_2=0\). Dann bleibt $$E \cdot I\cdot w(x) = \frac{q}{24}x^4 + \frac{C_1}{6}x^3 + C_3\cdot x$$ aus \(w(x=L)=0\) d.h. keine Durchbiegung im rechten Lager, folgt $$E \cdot I\cdot w(x=L) = \frac{q}{24}L^4 + \frac{C_1}{6}L^3 + C_3\cdot L = 0$$ $$ \space \Rightarrow \space \frac{q}{24}L^3 + \frac{C_1}{6}L^2 + C_3 = 0$$ aus \(w'(x=L)=0\) d.h. feste Einspannung im rechten Lager, folgt $$E \cdot I\cdot w'(x=L) = \frac{q}{6}L^3 + \frac{C_1}{2}L^2 + C_3 = 0$$ von dieser Gleichung ziehe ich die vorhergehende ab und erhalte $$ \frac{q}{8}L^3 + \frac{C_1}{3}L^2 = 0 \quad \Rightarrow \frac{q}{8}L + \frac{C_1}{3} = 0$$ $$\space \Rightarrow C_1 = \frac{-3}{8}qL$$ dann wäre das erste Deiner Ergebnisse bestätigt.
"Wenn ich aber folgende Bedingung nehme EIwIII(x=0)=C1=-q*L/2" Du behauptest, dass $$E \cdot I \cdot w'''(x=0) = \frac{-1}{2}qL$$ sein soll. Allgemein gilt, dass $$E \cdot I \cdot w''(x) = - M_y; \quad \quad E \cdot I \cdot w'''(x) = -Q_z$$ D.h. Deine Annahme ist, dass auf dem linken Lager die Hälfte der Gesamtlast \(q\cdot L\) liegen. Diese Annahme ist falsch! Sie ist falsch, weil die Lagerung statisch überbestimmt ist und ein Teil der Last auch über das Moment im biegesteifen rechte Lager gehalten wird. Die vertikale Lagerkraft ist rechts größer als links. Muss sie auch sein, um das Moment im rechten Lager auszugleichen. Das rechte Lager ist ein feste Einspannung und die nimmt auch ein Moment auf.
Gruß Werner