Ein Körper wird hoch geschleudert, im selben Moment beginnt anderer Körper zu fallen. Kreuzungspunkt berechnen

Question

Ein erster Körper wird mit der Anfangsgeschwindigkeit V₀ vertikal in die Höhe geschleudert. Im selben Moment beginnt ein zweiter Körper aus derjenigen Höhe h_s die der erste erreichen wird frei zu fallen. In welcher Höhe begegnen sich die beiden Körper? Berechnen sie auch eine numerische Lösung für V₀ = 16 m/s

Answer 1

hi

 

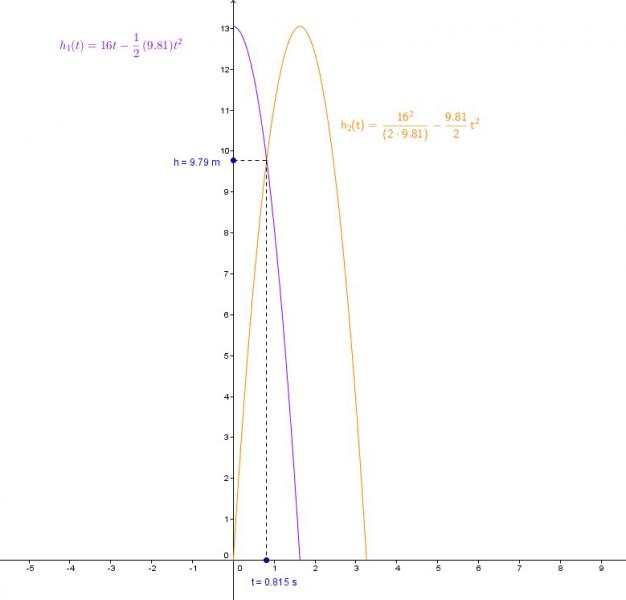
h1(t): zeitabhängige höhe des hochgeschleuderten körpers
h2(t): zeitabhängige höhe des fallengelassenen körpers
v₀²/(2g): maximale steighöhe des hochgeschleuderten körpers

h₁(t) = v₀ * t - g/2 t²
h₂(t) = v₀²/(2g) - g/2 t²

die körper begegnen sich auf gleicher höhe: h1(t) = h2(t)

h1(t) = h2(t)
v₀ * t - g/2 t² = v₀²/(2g) - g/2 t²
v₀ * t = v₀²/(2g)
t = v₀/(2g)

zum zeitpunkt t = v₀/(2g) befinden sich beide auf gleicher höhe.
das ist die höhe

h = v₀ * v₀/(2g) - g/2 • (v₀/(2g))²
h = v₀²/(2g) - g/2 • v₀²/(4g²)
h = v₀²/(2g) - v₀²/(8g)
h = 3v₀²/(8g)

die körper begegnen sich in der höhe
h = 3*16²/(8g) ≈ 9,79 m
 

Comments

gerne! ^^ :-)