Hallo,
gar nicht so einfach aus Deinem Verhau, Deine Gedanken heraus zu bekommen! Bei Deiner Lösung hast Du Dich bereits am Anfang mit den Vorzeichen vertan ... ich gehe das einfach mal unabhängig von Deiner Lösung durch.
Du fragst: "ich meine so, ich habe von links geschneiten was ich möchte wissen es ist egal wo ich beginne links oder rechts" Ja - das kannst Du Dir aussuchen. Wenn Du von links schneidest, brauchst Du vorher die Lagerkräfte nicht zu berechnen.
Wenn Du von links schneidest, zeigt \(Q\) nach oben, \(N\) nach links und das Moment \(M_b\) dreht mathematisch negativ. Am einfachsten ist der Verlauf der Normalkraft \(N\), es gilt \(N=-F\) und zwar unabhängig von \(x\). \(N\) ist eine Druckkraft.
Die Querkraft \(Q\) ist im Intervall \(x \in [0;a)\) gleich 0. Bei der Position \(x=a\) springt sie durch die äußere Kraft auf \(Q(x\ge a)=-2F\).
Das Moment betrachte ich mal genauer. Zunächst wieder im Intervall \(x \in [0;a)\)

Beachte die Vorzeichen. D.h. der Hebelarm \(\vec{r}\) von der Schnittstelle zum Ansatzpunkt der waagerechten Kraft in x, y und z ist
$$\vec{r} = \begin{pmatrix} -x\\ 0 \\ a\end{pmatrix}$$ Die Z-Koordinate zeigt nach unten, daher ist die dritte Koordinate positiv. Der Kraftvektor \(\vec{F}\) ist
$$\vec{F} = \begin{pmatrix} F\\ 0 \\ 0\end{pmatrix}$$ Und da das Moment \(M_b\) mathematisch negativ in diesem Koordinatensystem definiert ist, ist das Produkt aus Hebelarm mal Kraft = minus \(M_b\):
$$\vec{r} \times \vec{F} = \begin{pmatrix} -x\\ 0 \\ a\end{pmatrix} \times \begin{pmatrix} F\\ 0 \\ 0\end{pmatrix} = \begin{pmatrix} 0\\ aF \\ 0\end{pmatrix} = -M_b(x < a)$$ hinter der eingeleiteten vertikalen Kraft \(2F\) im Bereich \(x \ge a\) geht es wie folgt weiter:
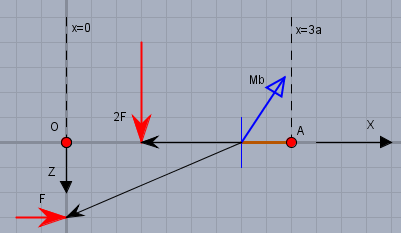
Das Moment aus der waagerechten Kraft bleibt und es kommt das Moment aus der vertikalen Kraft hinzu. Es ist:
$$\begin{aligned}-M_b(x \ge a) &= \begin{pmatrix} 0\\ aF \\ 0\end{pmatrix} + \begin{pmatrix} -(x-a)\\ 0 \\ 0\end{pmatrix} \times \begin{pmatrix} 0\\ 0 \\ 2F\end{pmatrix} \\& = \begin{pmatrix} 0\\ aF + 2F(x-a)\\ 0\end{pmatrix} = \begin{pmatrix} 0\\ F(2x-a)\\ 0\end{pmatrix} \end{aligned}$$ an der Stelle \(x=3a\) ist das Moment \(M_b\) dann
$$M_b(3a) = \begin{pmatrix} 0\\ -5aF\\ 0\end{pmatrix}$$ und der Verlauf von \(M_b(x)\) (genauer: seiner Y-Koordinate) sieht so aus
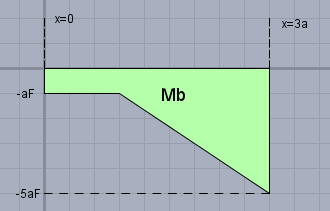
Gruß Werner
(Edit: bitte noch meinen unten stehenden Kommentar beachten)