Hallo Alonso,
Dein Freischnitt ist ok. Bei Fachwerken dieser Art berechnet man zunächst in einem Lager die Kräfte, die auf das Fachwerk wirken. Dafür kann man das ganze Fachwerk als starren Körper annehmen. Ich unterstelle es ist statisch bestimmt; dies ist aber hier der Fall. Ausgehend von einem Punkt in dem die Kräfte bekannt sind und in dem sich nur zwei Stäbe treffen berechnet man dann sukzessive alle Stabkräfte.
In diesem Fall kann man sich aber einiges vereinfachen, zumal nur einige der Stabkräfte berechnet werden sollen. Die Gesamtkraft ist \(16F\). Wegen der Symmetrie verteilt sich diese gleichmäßig auf die Lager \(A\) und \(B\). Also ist \(A_y=B_y= 8F\). Und da die Lagerkraft in \(A\) nur senkrecht zu den eingezeichneten \(45°\) wirken kann, ist auch \(A_x=A_Y=8F\).
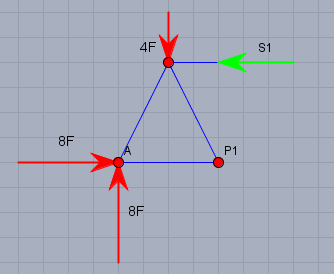
Oben habe ich \(S_1\) frei geschnitten und berechne \(S_1\) indem ich die Momente um \(P_1\) betrachte:
$$\sum M_{P1} = 0 = hS_1 + \frac{h}{2} \cdot 4 F - h\cdot 8F \quad \Rightarrow S_1=6F$$
Genauso kann man jetzt bei \(S_3\), \(S_4\) und \(S_6\) vorgehen:
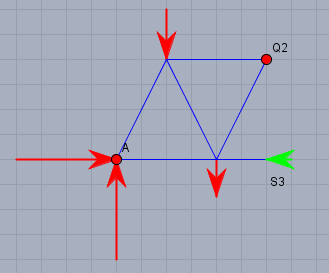
Die Summe der Momente um \(Q_2\) muss 0 sein. Ich habe \(S_3\) von rechts nach links wirkend eingezeichnet - also als Druckstab angenommen:
$$\sum M_{Q2}= h\cdot 8F - \frac32h \cdot 8F + h \cdot 4F + \frac{h}{2} \cdot 3F - h\cdot S_3 \quad \Rightarrow S_3 = \frac32 F$$
\(S_4\) und \(S_6\) solltest Du nun allein hin bekommen. Und \(S_2\) bekommt man über die Kräftesumme im Knoten \(Q_2\) (s.o.). Überleg' Dir das mal selber - es ist jetzt schon spät.
Gruß Werner