Physik. Arbeit einer Kugel berechnen, die angehoben wird

Question

Hallo :)

Ich weiß bei folgender Aufgabe nicht weiter:

Ich habe eine Kugel, die sich in einem Becken voller Wasser befindet. (Masse der Kugel 100g, Radius 2,8cm).  Die Temperatur des Wassers beträgt am Punkt x=0   20°  (dichte des Wassers 1000 Kg/m^3)

Am Boden des Beckens befindet sich eine Heizplatte wodurch die Temperatur sich mit der Tiefe um ΔT = -1K/m ändert.(Wärmeausdehnungskoeffizient α=21,8*10^-4)

Nun soll die Kugel von unten (x= -13 )angehoben werden auf (x=0) und die Arbeit dabei berechnet werden.

Eigentlich wird die Arbeit ja so berechnet

W=  m_kugel *g*h  -  V_kugel * ρ_{wasser *} g*h

aber das Volumen der Kugel ändert sich ja während des Auftauchens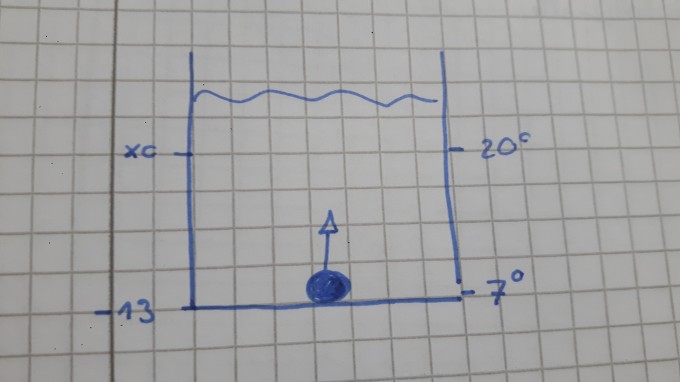 .....deswegen habe ich gedacht dass,

ich es so mache :  W= m_kugek *g*h-  ρ_wasser *g*h * ∫₇²⁰   V*(1- αT)^3 dT      

Aber da kommt nur Müll raus.... kann mir jemand erklären wie man es richtig macht?

Comments

aber das Volumen der Kugel ändert sich ja während des Auftauchens

Ich würde eher sagen, die Dichte des Wassers ändert sich während des Auftauchens.

mit dem Integral zu rechnen ist schon richtig. Allerdings eben mit der Dichte in Abhängigkeit von der Tiefe.

---

In der genauen Aufgabenstellung die ich bekommen habe wird deutlich gemacht, dass das hier nicht der Fall ist, sondern sich wirklich das Volumen der Kugel verändert.

---

Bestimme also zunächst mal die Formel für die Dichte in Abhängigkeit von x.

---

Masse der Kugel 100g, Radius 2,8cm

Der Radius der Kugel ist doch offensichtlich konstant. Wie kann sich dann das Volumen ändern welches sich aus

V = 4/3 * pi * r^3 ergibt?

Und auch das h sollte nachher nicht mehr in der Formel stehen da das ja durch das Integral über minimale Höhenänderungen ersetzt wird.

---

Ich dachte dass sich das Volumen der Kugel so ändert:

V(T) = V₀ *(1+α ΔT)

Und dass wollte ich integrieren.... das V₀ was ja 4/3 pi*r^3 hätte ich dann noch vor das Integral gezogen....

So dachte ich, dass es funktioniert... tut es aber nicht :(

---

Wie gesagt das Volumen der Kugel ist ebenso wie der Radius konstant. Nur die Dichte des Wassers ändert sich mit der Höhe. Und da solltest du jetzt mal eine Funktion aufstellen, welches die Dichte des Wassers in Abhängigkeit von x angibt.

---

Sorry ich weiß nicht wie das gehen sollte :( ,wobei doch auch wirklich wortwörtlich in meiner original Aufgabenstellung steht:" Die Dichte des Wassers bleibt dabei konstant. Die Kugel hingegen besteht aus einem "supermaterial" mit einem linearen Ausdehnungskoeffizient von 21,8*10^-4 1/K"

---

Wo stehst das in der obigen von dir geposteten Aufgabe? Kann es sein das du von 2 unterschiedlichen Aufgaben sprichst?

---

Nein, es tut mir leid, ich hatte die Aufgabe nur zusammen gefasst, da sie aus mehreren Teilaufgaben besteht.

---

Aus dem Grund ist es günstig immer die Aufgabe in der original Formulierung zu lassen. Denn so ist z.B. unklar bei welcher Temperatur der Radius der Kugel nun genau 2.8 cm beträgt.

Vielleicht fotografierst du nochmals die original Aufgabenstellung ab. Lege auch die Lösung bei, wenn du eine hast. Dann kann man dir am besten eine Hilfestellung geben.

---

 

Also hier ist die Originalaufgabenstellung und bis auf die d) konnte ich auch alle lösen. :)

---

Ich komme da etwa auf 0.523 J

Aber mal etwas anderes. bei x = 0 ist die Gewichtskraft höher als die Auftriebskraft also sinkt der Körper.

In 13 m Tiefe bei x = -13 ist der Körper Kräftefrei. D.h. Auftriebskraft = Gewichtskraft.

Damit das der Fall ist muss sich doch der Körper ausdehnen oder ?

Damit sich der Körper ausdehnt muss die Temperatur in der Tiefe größer sein als die an der Oberfläche?

Du hast bei dir am Boden eine Temperatur von 7 Grad eingezeichnet. Wo ist mein Denkfehler?

---

Echt? wie kommst du auf die 0,523J?

Ja das fand ich auch seltsam.....in der Aufgabenstellung steht ja eigentlich auch dass am Boden eine Heizplatte angebracht ist. Also hast du eigentlich schon recht. Nur war ich verwirrt, weil da auch steht dass sich die Temperatur mit der Tiefe sich um -1 K/m ändert.....also mit der Tiefe demnach die Temperatur fällt. Vielleicht ist aber das Minus ein Fehler in der Aufgabenstellung...

---

Ja. Da ist die Aufgabenstellung etwas irreführend. Denn mit Tiefe meint man ja eigentlich den Betrag des Höhenunterschiedes.

In der Aufgabe soll wohl -13 m die Angabe für die Tiefe sein. D.h. in -13 m Tiefe hat man dann eine höhere Temperatur.

Hier meine Rechnung zu d)

d)
FG·s = (0.981 N)·(13 m) = 12.753 J
FA(x) = (1000 kg/m^3)·(4/3·pi·((0.028 m)·(1 + (x m)·(-1 K/m)·(0.00218 1/K)))^3)·(9.81 N/kg)
∫ (-13 bis 0) (1000 kg/m^3)·(4/3·pi·((0.028 m)·(1 + (x m)·(-1 K/m)·(0.00218 1/K)))^3)·(9.81 N/kg) dx = 12.23 J
12.753 J - 12.23 J = 0.523 J

---

Ah! wenn ich das jetzt richtig verstehe, hast du nicht über die Temperatur dT, so wie ich es versucht habe integriert, sondern über die Höhe dx? Und ΔT hast du ausgedrückt als x*(-1K/m) ?

---

Sicher,dass du bei dem Integral auf 12,23J kommst?

ich bekomme da 11,89 J raus...

---

Ja. Eigentlich schon. Ich hab das so mit dem TR ausgerechnet.

∫ (-13 bis 0) 1000·(4/3·pi·(0.028·(1 + x·(-1)·0.00218))^3)·9.81 dx

Vereinfacht

∫ (-13 bis 0) 13080·pi·0.028^3·(1 - 0.00218·x)^3 dx

---

jetzt sehe ich was ich anders gemacht habe...

warum kann ich es nicht so machen?

∫(-13 bis 0) 1000 (4/3*pi*(0,028)^3)*(1-0,00218*x) dx

also warum muss man das ^3 vom Radius auch an den x-Ausdruck (1-0,00218*x) dran machen?

Answer 1

Das ist doch der Ausdruck für die Längenänderung des linearen Ausdehnungskoeffizienten. Die Längenänderung findet ja aber in den 3 Dimensionen Länge, Breite und Höhe statt. Wie konntest du c) berechnen wenn du die Formel verkehrt aufschreibst? Hattest du nicht gesagt dass du c) konntest?

Comments

stimmt, ja, sorry ich habe einfach nicht mehr an die hoch 3 in der Formel gedacht

Vielen, vielen Dank für die tolle  Hilfe und dass du nicht die Geduld mit mir verloren hast... :´D