Physik: Harmonische Schwingungen; maximaler Auslenkungswinkel beim Durchgang

Question

Guten Abend,

ich komme leider bei der Aufgabe 7e) auf diesem Blatt nicht mehr weiter. Wie kann ich denn hier den maximalen Auslenkungswinkel bestimmen?

Die Lösung am Rand steht ebenfalls dabei; allerdings ist mir aber nicht klar, wie man auf dieses Ergebnis kommt.

Ich würde mich sehr über eure Hilfe freuen :)

Viele Grüße

Answer 1

Hallo,

Der Energieverlust macht sich unmittelbar in der Schwingungshöhe des Pendels bemerkbar. Verliert das Pendel 10% Energie so schwingt es auch 10% weniger hoch, da die potentielle Energie direkt proportional zur Höhe ist.

 

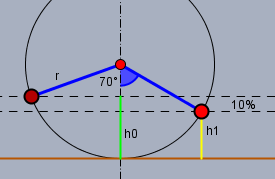
In obiger Skizze ist die Starthöhe $h_0$ grün eingezeichnet. Die gelbe Höhe $h_1$ ist um 10% kleiner. Es ist

$$h_0 = r(1- \cos 70°)$$

die Schwinghöhe $h_1$ nach einer Halbperiode ist $h_1 = 0,9 \cdot h_0$. Demnach ist der Kosinus von $\alpha$ (blau)

$$\cos \alpha = \frac{r - h_1}{r} = \frac{r(1 - 0,9 + 0,9 \cdot \cos 70°)}{r} = 0,1 + 0,9 \cdot \cos 70°$$

$$\space \Rightarrow \alpha \approx 65,9°$$

Ist nicht genau die Lösung, die Du angegeben hast, aber ungefähr.

Gruß Werner

Comments

Danke für die schnelle Antwort, allerdings verstehe ich nicht, wo das rechtwinklige Dreieck für den Cosinus ist?

Danke :)

---

Ich habe das rechtwinklige Dreieck um $\alpha$ (der blaue Winkel) rot eingezeichnet

$$\cos \alpha = \frac{r-h_1}{r}$$