Betrachte das Problem zunächst rein statisch.
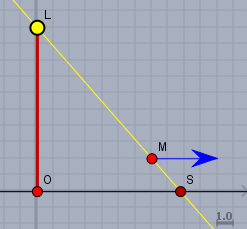
Der Lichtstrahl zur Spitze des Schattens geht von der Lampe \(L\) 'durch' die Spitze des Mannes \(M\) und trifft den Boden bei \(S\) - die Position der Schattenspitze. In vektorieller Darstellung dieses Strahls \(g\) kann man also schreiben:
$$g = L + (M-L) t$$
Die Ebenengleichung für den Boden (dort ist der Schatten) in der Hesseschen Normalform lautet
$$e_z \cdot x =0$$
und daraus lässt sich dann die Position der Spitze des Schattens \(S\) berechnen. Ich setze \(g\) für \(x\) ein:
$$e_z \cdot \left( L + (M-L) t\right) =0 \quad \Rightarrow t=\frac{e_z \cdot L}{e_z \cdot (L-M)}$$
so bekommt man das \(t\) und daraus folgt die Position für \(S\) nach Einsetzen in die Gleichung des Lichtstrahls:
$$S = L + (M-L) \frac{e_z \cdot L}{e_z \cdot (L-M)}$$
Es ist Dir vielleicht aufgefallen, dass ich bisher nicht festgelegt habe, ob es sich um ein 2- oder 3-dimensionales Problem handelt. Vielleicht scheint Dir der Weg bisher zu 'kompliziert'. Aber ich habe ihn mit Absicht gewählt, um den 2.Fall (Laterne nicht im Rücken des Mannes) gleich mit zu behandeln.
Nehmen wir mal den einfachen Fall (Laterne im Rücken des Mannes), dann liegen alle Positionen in einer Ebene so wie in der Skizze oben. Die Laterne stehe an der Position 0 und der Mann befinde sich bei \(x\) - also ist
$$L=\begin{pmatrix} 0 \\ h_L \end{pmatrix}; \space M= \begin{pmatrix} x \\ h_M \end{pmatrix}$$
Einsetzen in die Gleichung für S ergibt
$$S = \begin{pmatrix} 0 \\ h_L \end{pmatrix} + \begin{pmatrix} x \\ h_M - h_L \end{pmatrix} \frac{h_L}{h_L - h_M}=\begin{pmatrix} 0 \\ 10 \end{pmatrix} + \begin{pmatrix} x \\ -8 \end{pmatrix} \frac{10}{8}=\begin{pmatrix} \frac{5}{4}x \\ 0 \end{pmatrix} $$
Es ist keine Überraschung, dass die Z-Koordinate immer =0 ist und die Schattenspitze liegt immer um den Faktor 5/4 vor dem Mann. Die Geschwindikeit ist die Ableitung nach der Zeit -also kommt man zur Geschwindigkeit \(v_s\) der Schattenspitze:
$$\dot S = \vec{v_S}= \begin{pmatrix} \frac{5}{4} \dot x \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{5}{4} v \\ 0 \end{pmatrix} = \frac{5}{4} \begin{pmatrix} v \\ 0 \end{pmatrix}= \frac{5}{4}\vec{v}$$
oder auch, wenn man die Bewegung in nur einer Dimension betrachtet
$$v_S=\frac{5}{4} v$$
Der Übergang in das 3-dimensionale ist jetzt trivial. Betrachte die Variable \(x\) einfach als 2-dimensionale Position auf dem Boden und deren Ableitung nach der Zeit als die Geschwindigkeit \(\vec{v}\) des Mannes. Ich übernehme einfach, was schon oben steht:
$$\vec{v_S}=\frac{5}{4} \vec{v}$$