oswald schrieb: "Nein, hier kennt sich niemand mit Statik aus. Wir machen hier nur Analysis und lineare Algebra."
Nicht so bescheiden. Ich denke, dass die Menge aller Fähigkeiten der Antwortenden in diesem Forum mehr umfasst als nur Analysis und lineare Algebra ;-). Hier reicht doch ein Minimum an Mechanik und etwas Vektorrechnung bzw. Trigonometrie.
\(G\) sei hier das Gewicht des Autos.
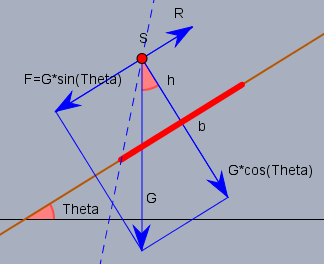
Das Auto rutscht nicht, solange die Reibkraft \(R= \mu_H \cdot G \cdot \cos \Theta\) nicht kleiner ist als die Kraft \(F\), die das Auto das Bankett hinunterrutschen lässt - also \(F=G \cdot \sin \Theta\). Die Bedingung ist demnach
$$G \cdot \sin \Theta \le \mu_H \cdot G \cdot \cos \Theta \quad \Rightarrow \Theta \le \arctan \mu_H \approx 21,8°$$
Das Auto kippt nicht, solange die Wirklinie der Gewichtskraft durch die Standstrecke \(b\) des Autos verläuft. Die Bedingung ist
$$\frac{b}{2h} \ge \tan \Theta \quad \Rightarrow \Theta \le \arctan \left( \frac{b}{2h} \right) = 45°$$
Der kleinere Wert für \(\Theta\) ist natürlich der entscheidende. D.h. das Auto rutscht bevor es kippt. Die Geschwindikeit und das Gewicht spielen wie man sieht keine Rolle. In der Praxis wird die Geschwindigkeit aber den Wert für \(\mu_H\) beeinflussen.