Baum und Teilbäume. BBD vereinfachen. Regeln

Question

Aufgabe:

Reduzieren Sie das BDD schrittweise soweit wie möglich, indem Sie jeweils eine der beiden Vereinfachungsregeln anwenden. Markieren Sie im BDD den Teil, auf den Sie die Regel angewendet haben und zeichnen Sie das BDD nach jedem Schritt neu.

Comments

EDIT: Wie kommt es zum Tag "Physik" ? Hast du inzwischen vielleicht einen besseren Vorschlag? 

Gibt es eine konkrete Fragestellung? Woher kommt die rote Linie? 

Answer 1

Antwort mit KI erzeugt

Schritt 1: Startsituation

Zu Beginn haben wir ein Binäres Entscheidungsdiagramm (BDD), das wie folgt aussieht:



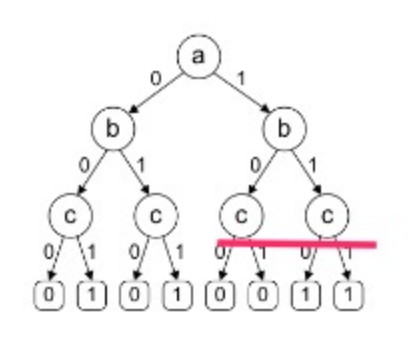
Regeln zur Vereinfachung eines BDD

1. Entfernung redundanter Knoten: Wenn ein Knoten zwei identische Unterknoten hat, kann dieser Knoten entfernt werden, und die Verbindung geht direkt zu dem gemeinsamen Unterknoten.
2. Vereinigung isomorpher Teilbäume: Wenn zwei Teilbäume identisch sind, können sie durch einen einzigen Teilbaum ersetzt werden.

Schrittweise Reduktion

Es ist wichtig festzustellen, dass ohne die genaue Struktur des BDD aus dem Bild zu kennen (da ich das Bild nicht sehen kann), die folgende Antwort einen allgemeinen Ansatz zur Vereinfachung eines BDD darstellt.

Schritt 2: Anwenden der ersten Vereinfachungsregel

Suche nach einem Knoten, der zwei identische Unterknoten hat. Angenommen, es gibt einen Knoten \(A\) im BDD, der zwei Pfade zu einem identischen Knoten \(B\) hat. Wir würden diesen Knoten entfernen und die Verbindung direkt von \(A\) zu \(B\) führen.

Schritt 3: Wiederholung mit Vereinigung isomorpher Teilbäume

Nach der Entfernung redundanter Knoten suchen wir nach isomorphen Teilbäumen, also identischen Strukturen im Diagramm. Wenn wir beispielsweise zwei identische Teilbäume finden, die von Knoten \(C\) und \(D\) ausgehen, würden wir diese durch einen einzigen Teilbaum ersetzen, der von beiden Knoten \(C\) und \(D\) geteilt wird.

Fortlaufende Wiederholung

Diese Schritte wiederholen wir fortlaufend, bis keine weiteren Vereinfachungen mehr möglich sind. In jedem Schritt:

1. Prüfen auf redundante Knoten und deren Entfernung
2. Suchen nach isomorphen Teilbäumen und deren Vereinigung

Endzustand

Das Endergebnis wäre ein vereinfachtes BDD, das die gleiche logische Funktion wie das ursprüngliche Diagramm darstellt, aber effizienter in Bezug auf die Knotenanzahl und Struktur ist.

Ohne das spezifische BDD-Bild zu analysieren, ist es schwer, exakte Schritte und das Endergebnis zu benennen. Die Anwendung dieser allgemeinen Regeln sollte jedoch auf jeden Fall zur Reduktion und Optimierung des gegebenen BDD führen.