Betrag vom Feld im Ringmittelpunkt

Question

Ich komme einfach nicht auf die richtige Lösung bei b)

Meiner Meinung nach müsste man einfach integrieren könne, mit der Formel des elektrischen Feldes:

leider kommt man da beim Integral (und dem ganzen Term) auf 0, was ja mathematisch auch Sinn macht, nur wie ich es besser machen könnte fällt mir nicht ein.

Freue mich über jegliche Tipps.

Danke!

Answer 1

Anstatt einfach eine Formel nach dem Zufallsprinzip hinzuschmeissen, wuerde ich es mit einer Herleitung probieren. Ein Ringelement \(d\ell\) gibt einen Beitrag \(d\vec{E}\) wie folgt zum Feld im Mittelpunkt: $$d\vec{E}=-\frac{\lambda_0\sin\phi\,d\ell}{4\pi\epsilon_0r^3}\vec{r}.$$ Diese Groesse muss jetzt ueber den Ring integriert werden.

Comments

Hallo, danke für deine Antwort!

Darf ich fragen wie du auf

$$ \frac{\overrightarrow{r}}{r^3} $$

gekommen bist anstelle von

$$ \frac{1}{r^2} $$

?

Vielen Dank!

---

\(-\vec{r}/r\) ist die normierte Richtung von \(d\vec{E}\).

---

Okay, das macht Sinn! Deine Formel habe ich komplett verstanden.

Ich veruche gerade zu verstehen wie ich über den Ring integriere .. nur ist dort ja wieder phi (bzw. bei dir l) die einzige Veränderliche, und wenn ich einmal rum gehe (0 bis 2pi) lande ich wieder beim Anfang, was mir ja bei der Integration wieder eine 0 zurück gibt .. verstehst du mein Problem? Ich habe sicherlich einen Denkfehler, ich würde mich sehr freuen wenn du nochmal erläutern könntest wie ich vorgehen muss / was ich falsch mache.

Danke!

---

Druecke \(d\ell\) mit \(d\phi\) aus und schreibe eine Formel für \(\vec{r}=\vec{r}(\phi)\) hin. Hast Du schon die obligatorische Skizze gemacht, in der diese Groessen alle eingezeichnet sind? Nein? Dann wird's Zeit!

---

Das habe ich bisher.

Bei r bin ich mir eigentlich sicher, dass ich es richtig gemacht habe, aber dl? Ist ja eigentlich das gleiche, allerdings wird ja auch gerade dadurch der Kreis beschrieben .. ? Ich stehe gerade ziemlich auf dem Schlauch.

Die Skizze habe ich so gut ging mit dem was ich habe gemacht, ich bin mir aber nicht sicher ob du darauf abgezielt hast.

---

Der Kreis ist kein Einheitskreis, sondern er hat den Radius \(r\), der auch \(\ne1\) sein darf. \(\vec{r}\) ist ein Vektor vom Nullpunkt aus zu dem Kreispunkt, der zum Linienelement \(dl\) gehoert. \(dl\) ist ein Stueckchen von der Kreisperipherie. Die Laenge davon entspricht (fuer \(r\ne1\)) nicht dem Winkelinkrement \(d\phi\) im Bogenmass.

---

Du hast recht! Wie sieht es jetzt aus?

Ich verstehe glaube ich noch gar nicht richtig was dl repräsentiert. Wenn du von der Länge redest kommt mir direkt $$ \phi{}r_R $$ in den Kopf, also $$ 2\pi{}r / 2\pi{} * \phi, \phi \in [0, 2\pi]$$ (aus der Formel des Kreisumfangs umgeformt für Teilstücke des Kreisumfangs)

---

\(dl\) ist ein infinitesimales Stuecken von der Kreislinie, bzw. es steht für dessen Laenge, weil nur die interessiert. Auf diesem Linienelement sitzt die Ladung \(dq=\lambda\,dl\), die man ins Coulombsche Gesetz eingetragen hat.

Da hast Du ein Bild: http://www.tm-mathe.de/Themen/fungr/bogenpolar.gif

Das rote Kurvenstueck da entspricht \(dl\), wenn man es sich unendlich klein denkt. Entsprechend \(d\phi=\phi_2-\phi_1\). Bei uns ist die Kurve ein Kreis, im Bild nicht. Gefragt ist jetzt noch, wie man bei einem Kreis \(dl\) aus \(d\phi\) bekommt.

---

Danke für die Erläuterung!

Aber ist das nicht gerade $$ \phi{}r_R $$ ?

Denn ein Kreis mit r=2 hat einen Umfang von $$ 2\pi{}*2 $$ was gleichwertig ist mit $$ \phi{}*2 ,  \phi=2\pi $$

---

Gib doch einfach die gesuchte Relation zwischen \(d\ell\) und \(d\phi\) an. Natuerlich steckt da nur Elementargeometrie dahinter.

Wenn Du's hast, kannst \(d\vec{E}\) so schreiben, dass alles nur noch von \(\phi\) abhaengt, und das Integral ausrechnen.

---

Leider komme ich noch immer nicht zum richtigen Ergebnis. Solange sin(phi) im Term steht und ich von 0 bis 2pi integriere wird doch immer 0 rauskommen?

Wo liegt diesmal der Denkfehler?

Zum Thema dl: Ich kann mir dl als d_phi ausgedrückt nur als phi*r vorstellen, wieso stimmt das denn nicht? Damit gibt man doch gerade die Länge an ..

Danke!

---

..........................................

---

Diesen Zusammenhang habe ich verstanden, und hier ist dl = d_phi*r, wobei ich davon ausgegangen bin, dass der Winkel phi und nicht d_phi ist.

wenn phi = pi dann ist dl = pi*r, das müsste doch stimmen?

---

Diesen Zusammenhang habe ich verstanden, und hier ist dl = d_phi*r, wobei ...

Nix wobei. Die Sache ist hier zu Ende: \(d\ell=r\,d\phi\).

---

Okay! Damit habe ich dann das r in das Integral gezogen, dort wird ja über d_phi integriert.

Allerdings habe ich es dann auch direkt wieder herausgezogen, da r ja keine Integrationskonstante ist. Im Term vor dem Integral steht daher nur noch r^2 im Nenner.

Trotzdem bleibt das Problem, dass sin(phi) bei mir 0 wird wenn ich 2pi und 0 einsetze.

Ich danke dir, dass du dir so lange für mich Zeit nimmst.

---

Ich glaube ich hatte gerade einen Geistesblitz.

Ist dies die gefragte Lösung?

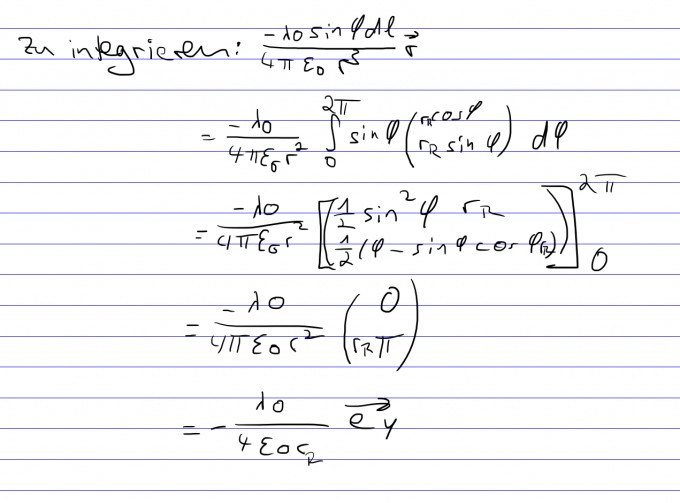
(das r_R soll hier nicht in den Klammern der y-Komponente des Vektors stehen)

Falls ja, ist die Lösung zu (a) einfach -ey (Vektor)?

Bin nur etwas verunsichert da ja nach einem Betrag gefragt ist, und hier ist ja auch eine Richtung mit angegeben.

Daaanke nochmal für die Hilfe!

---

\(r_R=r\). Du musst Dich halt entscheiden, was Du schreiben willst, und dann dabei bleiben. Die Aufgabenstellung schlaegt \(r_R\) vor.

Ansonsten: Dein Ergebnis hat doch Betrag und Richtung. Damit kannst Du beide Fragen beantworten.

Answer 2

Das Feld zeigt übrigens meiner Meinung nach in $$ -\overrightarrow{e_y} $$ Richtung. (Ich bin der Fragensteller)