Hallo,
Zunächst zeichne ich alle Kräfte ein, die auf den Stützträger wirken. \(F_D\) ist die Kraft, mit der das Drahtseils auf den Träger einwirkt, \(F_B\) ist die Kraft, die das Gelenk auf den Träger ausübt, und \(F_3\) und \(F_G\) sind die Gewichtskräfte des Trägers selbst und des Betonblocks.
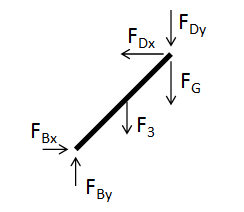
Ich habe sie in den Richtungen eingezeichnet, wie sie wahrscheinlich auch wirken. Also ist z.B. \(F_{Bx}\) nach rechts positiv und \(F_{Dx}\) ist nach links positiv. Die Richtung des Drahtseils ist vorgegeben. Damit ist
$$\frac{F_{Dy}}{F_{Dx}}=\tan {30°}$$
Aus der Tatsache, dass sie Summe aller Kräfte immer =0 ist, folgt dann
$$F_{Bx}=F_{Dx}$$
$$F_{By}=F_3 + F_G + F_{Dy}$$
Die Momente um das Gelenk müssen in Summe =0 sein - also ist
$$(F_{Dy} + F_G + \frac{1}{2}F_3)\cdot r= F_{Dx}\cdot r$$
\(r\) sei der Abstand des Trägerendes vom Gelenk in horizontaler und vertikaler Richtung. Da der Winkel des Träges gegenüber der Horizontalen gleich \(45°\) ist, ist dieser in beiden Richtungen gleich.
Das sind vier Gleichungen mit vier Unbekannten, die Du wahrscheinlich selbst lösen kannst (\(r\) fällt gleich raus). Z.B. für \(F_{Dx}\) ergibt sich
$$F_{Dx}=\frac{F_G+\frac{1}{2}F_3}{1-\tan {30°}} \approx 585,6 \text{kp} \approx 5743 \text{N}$$
und \(F_D\) ist dann
$$F_D=\frac{F_{Dx}}{\cos{30°}} \approx 676,2 \text{kp} \approx 6631 \text{N}$$
Falls noch Fragen offen bleiben, so melde Dich bitte.