Schwingungsdauer der gedämpften Schwingung

Question

Hallo Leute,

wie kommt man auf die Schwingungsdauer der gedämpften Schwingung?

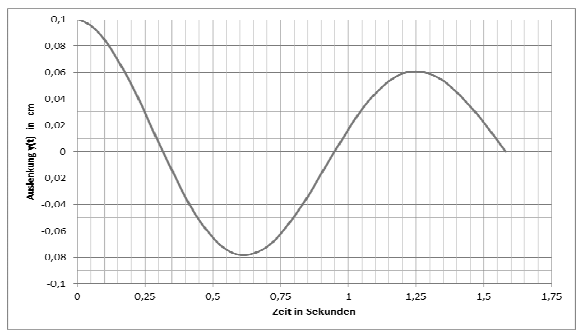
Gegeben wurde nur der Graph unten und die Masse = 2kg

Die Werte die ich habe:

Amplitude = 0,1 cm

To = 1,25s

fo = 1/To = 0,8Hz

wo = fo * 2pi = 1,6 pi

$$ { f }_{ 0 } =\frac { 1 }{ 2 \pi }  \sqrt { \frac { k }{ m }  }  $$

$$ 0,8\quad =\frac { 1 }{ 2\pi  } \sqrt { \frac { k }{ 2kg }  } |*2\pi  $$

$$ 1,6\pi\quad =\sqrt { \frac { k }{ 2kg }  }  | ()^2$$

$$ 2,56\pi^2\quad =\frac { k }{ 2kg }  |*2kg $$

$$ 2,56\pi ^{ 2 }\quad 2kg\quad =\quad k\quad \approx \quad 50,53kg $$

Wie komme ich auf Td, was mache ich falsch bei der Berechnung von k?

Answer 1

"wie kommt man auf die Schwingungsdauer der gedämpften Schwingung?"

To = 1,25s

Du hast doch den Wert schon aus der Zeichnung abgelesen!

Answer 2

Hallo,

die gedämpfte Schwingungsgleichung (hier ohne Phasenverschiebung) lautet:

y(t)=y₀*e^-δt*cos(w₀t) ,wobei δ die Abklingkonstante und w₀ die Kreisfrequenz der ungedämpften Schwingung ist.

Für die  gedämpfte Kreisfrequenz und gedämpfte Periodendauer gilt dann:

$$ { \omega }_{ d }=\sqrt { { \omega }_{ 0 }^2-\delta^2 }\\{ T }_{ d }=\frac { 2\pi }{ \sqrt { { \omega }_{ 0 }^2-\delta^2 } }\\{ T }_{ d }=\frac { 2\pi }{ \sqrt { \frac { 4\pi^2 }{ { T^2 }_{ 0 } }-\delta^2 } } $$

T₀=1.25 s hast du bereit aus dem Diagramm richtig abgelesen. Berechne mithilfe des Diagramms auch noch δ und setzte in die obrige Formel ein um die gedämpfte Schwingungsdauer zu berechnen.

Comments

Ich habe oben einen Fehler,die Schwingungsgleichung lautet

y(t)=y₀*e^-δt*cos(w_dt) 

Du kannst T_d schon ablesen. Das andere was ich geschrieben hab brauchst du nicht zu machen.