Physik Aufgabe Gravitationspotential

Question

Bis zu welcher Höhe h₁ über der Erdoberfläche darf man die potentielle Energie E_pot nach der
Formel E_pot = mgh berechnen, ohne dass der Fehler gegenüber der exakten Rechnung mit
Hilfe des Gravitationspotentials größer als 3% wird?
(Gravitationskonstante: γ=6,67*10^-11m^3kg^{-1}s^{-2}, Fallbeschleunigung: g = 9,81 m/s^2, Masse der
Erde: m_E=5,98*10^24 kg, Erdradius: r_E=6,37*10^6m

Ich habe keine gute Idee...ich weiß, dass die Formel E_pot = mgh nur im Spezialfall eines homogenen Kraftfeldes gilt, also bspw. für ein Kraftfeld, wie wir es hier auf der Erdoberfläche haben. Sobald eine bestimmte Höhe erreicht ist, entfernen wir uns aus dem homogenen Kraftfeld und somit ist die Formel keine gute Annäherung mehr zum bestimmen der pot. Energie. Die Genauigkeit der Formel nimmt mit steigender Höhe ab.

Viel mehr kann ich dazu gerade noch nicht sagen, würde mich über Tipps und Anregungen sehr freuen?

Comments

Hallo,

versuch doch mal g(h) zu berechnen, d.h. den Betrag der Erdbeschleunigung g in Abhängigkeit von der Höhe aus der Formel der Gravitationskraft. Das sollte hier mit Gravitationspotential gemeint sein.

Da die eine Masse (z.B. ein Mensch) in Relation zur anderen Mass (Erde) sehr klein ist, kann man sie in der Formel auch komplett vernachlässigen.

Danach stellt sich also nur noch die Frage ab welcher Höhe, deine ein 3% Unterschied zur Standard Erdbeschleunigung g gegeben ist.

Gruß

Answer 1

Hier meine Meinung

Die Erdanziehung verringert sich im Abstand zur Erde.

Hier ein Vergleich mit der Leuchtkraft einer Lichtquelle



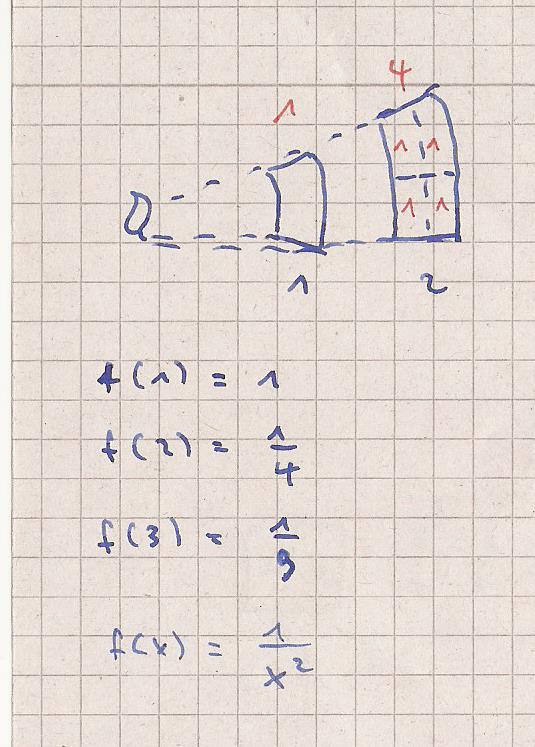
In der Mitte ist eine Kerze. Die Leuchtkraft der Kerze fällt in der
Entfernung 1 auf eine Fläche 1. In der Entfernung 2 fällt die Leuchtkraft
bereits auf eine Fläche von 4.
Dies ist bedingt durch die Vergrößung der Kugeloberfläche mit
O = 4 * π * r^2
Für Gravitationsfeld gilt genau dasselbe.
Die Stärke einer Leucht- oder Gravitationskraft wird beschrieben mit
f ( x ) = 1/ x^2

Jetzt müssen wir den Erdradius einbauen
r = 6,37*10⁶ m ( ich habe obigen Wert einmal verwendet
und rechnen um
r = 6,37*10⁶ m soll 1 sein
r = 2 * 6,37*10⁶ m soll 2 sein

f ( r ) = 1 / ( r / 6,37*10⁶ )^2

Wir wissen außerdem
g ist bei 6.37^10^6 gleich 9.81 m/s^2

Wir können die Erdbeschleunigung berechnen mit
g ( r ) = 9.81 / ( r / 6,37*10⁶ )^2
Im einfachen Abstand
g ( 6.37*10^6 ) =  9.81 / ( 6.37*10^6 / 6,37*10⁶ )^2 = 9.81 m/s^2
Im 2-fachen Abstand
g ( 2 * 6.37*10^6 ) =  9.81 / ( 2 * 6.37*10^6 / 6,37*10⁶ )^2 = 9.81 / 4 = 2.45 m/s^2

Nun zu
E_pot = m* g * h
m bleibt konstant
g ist g von  r : g ( r )
an der Erdoberfläche : h = 0
h ist etwas höher : h

E ( r ) = m * g ( r ) * r 
E ( r + h ) = m * g ( r + h ) * ( r  + h )

Jetzt muß ich einmal etwas handschriftlich schreiben
sonst wird es zu unübersichtlich.

Comments

Hier die weiteren Berechnungen

Bei Fehlerhinweisen oder Fragen melden.