Aufgabe:
Wieso funktioniert der orangene Weg nicht? R1 und R2 sind doch auch parallel geschaltet. 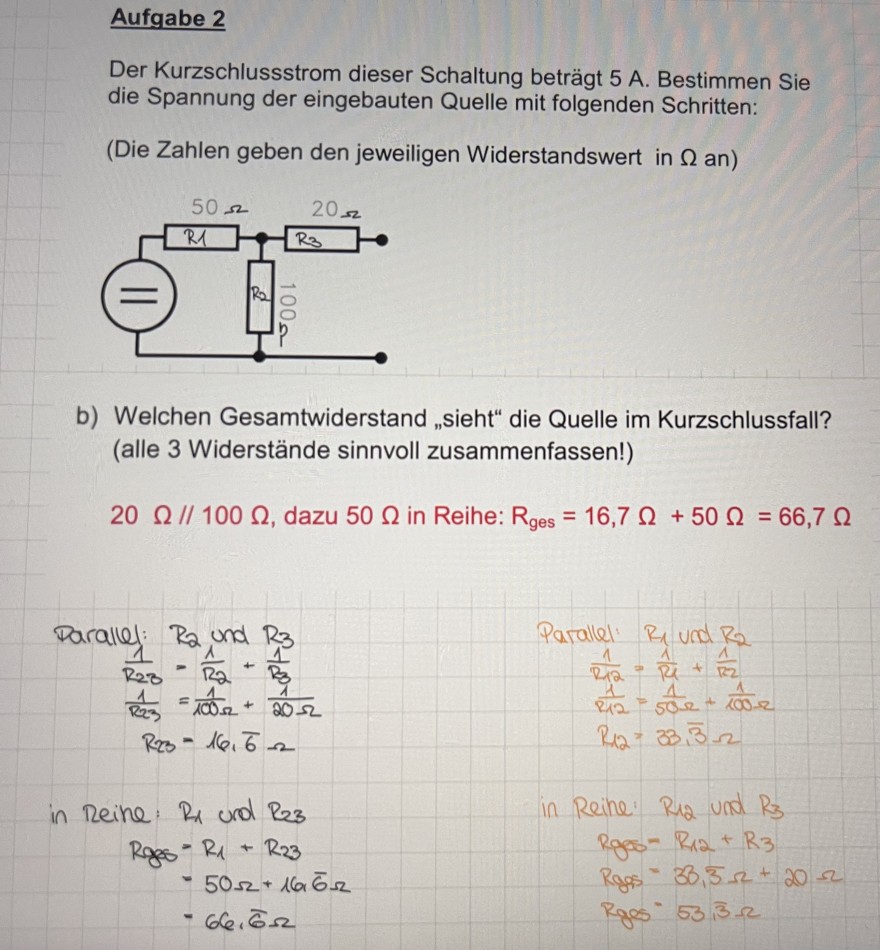
Text erkannt:
Aufgabe 2
Der Kurzschlussstrom dieser Schaltung beträgt 5 A . Bestimmen Sie die Spannung der eingebauten Quelle mit folgenden Schritten:
(Die Zahlen geben den jeweiligen Widerstandswert in \( \Omega \) an)
b) Welchen Gesamtwiderstand „sieht" die Quelle im Kurzschlussfall? (alle 3 Widerstände sinnvoll zusammenfassen!)
\( 20 \Omega / / 100 \Omega \), dazu \( 50 \Omega \) in Reihe: \( R_{\text {ges }}=16,7 \Omega+50 \Omega=66,7 \Omega \)
Paralle: \( R_{2} \) und \( R_{3} \)
\( \begin{array}{l} \frac{1}{R_{23}}=\frac{1}{R_{2}}+\frac{1}{R_{3}} \\ \frac{1}{R_{23}}=\frac{1}{100 \Omega}+\frac{1}{20 \Omega} \\ R_{23}=16, \overline{6} \Omega \end{array} \)
in Reine: \( R_{1} \) urd \( R_{23} \)
\( \begin{aligned} R_{\text {ges }} & =R_{1}+R_{23} \\ & =50 \Omega+16, \overline{6} \Omega \\ & =66, \overline{6} \Omega \end{aligned} \)
Paralle: \( R_{1} \) und \( R_{2} \)
\( \begin{array}{l} \frac{1}{R_{12}}=\frac{1}{R_{1}}+\frac{1}{1 R 2} \\ \frac{1}{R 2}=\frac{1}{50 \Omega}+\frac{1}{100} \Omega \\ R_{12}=33, \overline{3} \Omega \end{array} \)
in Reine \( R_{12} \) und \( R_{3} \)
\( \begin{array}{l} R_{g e s}-R_{12}+R_{3} \\ R_{\text {ogs }}-36,3 \Omega+20 \Omega \end{array} \)
\( \text { Rges - } 53, \overline{3} \Omega \)