Aufgabe:
Hallo! ich habe bereits einen Beitrag reingestellt und die Hilfestellungen wahrgenommen und versucht die folgende Aufgabe zu bewältigen! Es sind I1, I2 und I3 gesucht, wobei die Widerstände und der Wert der Quellspannung bereits angegeben sind!
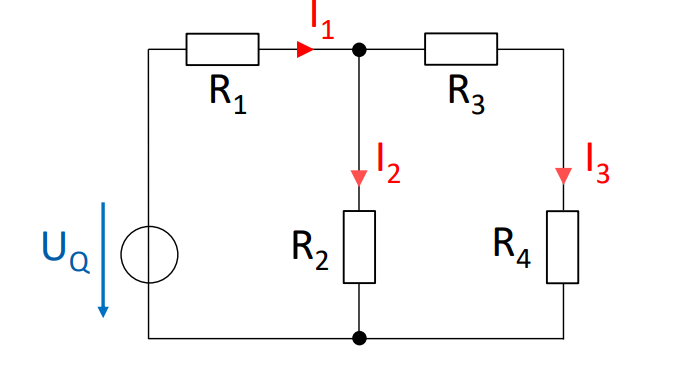
Problem/Ansatz:
Meine bisherige Lösung ist auch hier zusehen. Kann sich dieses wer anschauen?
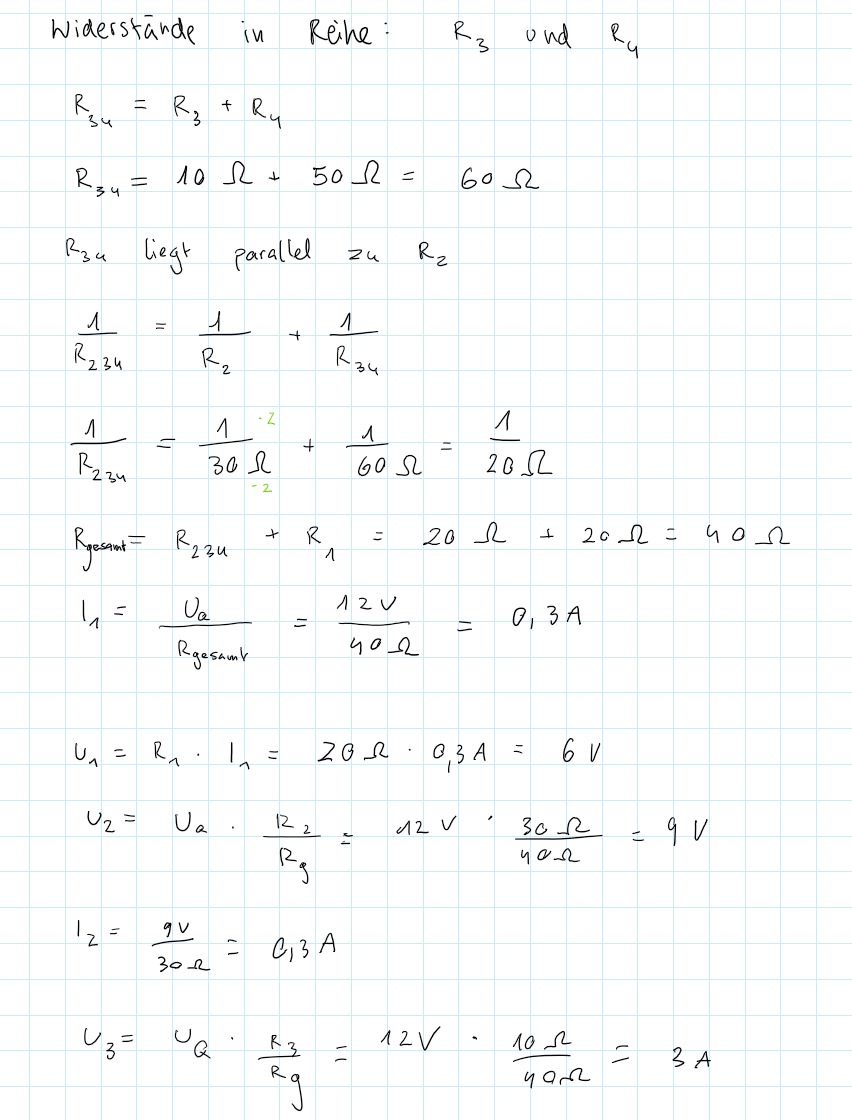
Text erkannt:
Widerstände in Reine: \( \quad R_{3} \) und \( R_{4} \)
\( \begin{array}{l} R_{34}=R_{3}+R_{4} \\ R_{34}=10 \Omega+50 \Omega=60 \Omega \end{array} \)
\( R_{3 u} \) liegt parallel zu \( R_{2} \)
\( \begin{array}{l} \frac{1}{R_{234}}=\frac{1}{R_{2}}+\frac{1}{R_{34}} \\ \frac{1}{R_{234}}=\frac{1}{30 \Omega}+\frac{1}{60 \Omega}=\frac{1}{20 \Omega} \\ R_{\text {gecant }}=R_{234}+R_{1}=20 \Omega+20 \Omega=40 \Omega \\ I_{1}=\frac{U_{a}}{R_{\text {gesaml }}}=\frac{12 \mathrm{~V}}{40 \Omega}=0,3 \mathrm{~A} \\ U_{1}=R_{1} \cdot I_{1}=20 \Omega \cdot 0,3 \mathrm{~A}=6 \mathrm{~V} \\ U_{2}=U_{a} \cdot \frac{R_{2}}{R_{g}}=12 \mathrm{~V} \cdot \frac{30 \Omega}{40 \Omega}=9 \mathrm{~V} \\ I_{2}=\frac{9 \mathrm{~V}}{30 \Omega}=0_{13} \mathrm{~A} \\ U_{3}=U_{Q} \cdot \frac{R_{3}}{R_{\mathrm{g}}}=12 \mathrm{~V} \cdot \frac{10 \Omega}{4 a \Omega}=3 \mathrm{~A} \end{array} \)
Nachtrag: mir fällt grad auf, dass mir I3 fehlt, aber ich bezweifle trotzdem, dass dje Berechnung der anderen Werte stimmt, weshalb es super wäre, wenn es sich wer anschauen könnte!!