
Text erkannt:
Aufgabe 3 Schraubenfeder (21 Punkte)
Eine warmgeformte (warmgewalzte) Druckfeder aus geschliffenem Rundstab mit \( d=18 \mathrm{~mm}, i_{\mathrm{f}}=7, D_{\mathrm{e}}= \) \( 90 \mathrm{~mm}, c_{1}=202 \mathrm{~N} / \mathrm{mm} \) soll abwechselnd mit \( F_{1}=5000 \mathrm{~N} \) und \( F_{2}=F_{\mathrm{n}}=10000 \mathrm{~N} \) belastet werden.
a) Berechnen Sie die Summe der Mindestabstände \( S_{\mathrm{a}} \), die Gesamtzahl der Windungen \( i_{\mathrm{g}} \), die Blocklänge \( L_{c} \), die beiden Federwege \( s_{1} \) und \( s_{2} \). Wie groß ist die Länge \( L_{0} \) der unbelasteten Feder? (6 Punkte)
b) Berechnen Sie die gleichmäßig verteilte Spannung \( \tau_{1} \) und weisen Sie die Festigkeit bei statischer Beanspruchung durch die \( \mathrm{Kraft} F_{1} \) nach. \( \Delta s=10 \mathrm{~mm} \). (8 Punkte)
c) Die warmgeformte Druckfeder mit einer Federsteifigkeit von \( c_{1}=202 \mathrm{~N} / \mathrm{mm} \) wird anschließend nur mit der Kraft \( F_{1} \) belastet. Allerdings wird zu ihr nach einem Federweg \( s \) von 10 mm eine zweite Feder mit einer Federsteifigkeit \( c_{2}=150 \mathrm{~N} / \mathrm{mm} \) parallel geschaltet (siehe Abbildung 4). Berechnen Sie die Gesamtsteifigkeit \( c_{3} \) der beiden Federn. Die beiden Federn werden bis Stauchung auf Blocklänge weiterhin mit der Kraft \( F_{1} \) belastet. Zeichnen Sie die Federkennlinie des Federpakets. Beschriften Sie die Achsen! (7 Punkte)
Abbildung 4: Federpaket
Problem/Ansatz:
a)
\( \begin{array}{l} S_{a}=0,02 \cdot D_{e} \because f=0,02 \cdot 90 \mathrm{~mm} \cdot 7 \\ S_{a}=12,6 \mathrm{~mm} \\ L_{0}=L_{c}+S a+S n \\ =147,6 \mathrm{~mm}+12,6 \mathrm{mm-1} \\ i g=i f+1,5=7+1,5=8,5 \\ L_{c}=(i g-0,3) \cdot d=(8,5-0,3) \cdot 18 \mathrm{~mm}=147,6 \mathrm{~mm} \\ s_{1}=\frac{F_{1}}{C}=\frac{5000 \mathrm{~N}}{202 \mathrm{~N} / \mathrm{mm}} \\ s_{2}=\frac{F_{2}}{C}=\frac{10000 \mathrm{~N}}{202 \mathrm{~N} / \mathrm{mm}} \\ s 1=24,75 \mathrm{~mm} \\ s q=49,5 \mathrm{~mm} \\ L_{0}=L_{c}+S a+s n=147,6 \mathrm{~mm}+12,6 \mathrm{~mm}+49,5 \mathrm{~mm} \\ L_{0}=209,7 \mathrm{~mm} \\ \end{array} \)
b)
\( \begin{array}{l} D=D e-d=90 \mathrm{~mm}-18 \mathrm{~mm}=72 \mathrm{~mm} \\ \tau_{i}=\frac{8 \cdot D \cdot F}{\pi \cdot d^{3}}=\frac{8 \cdot 72 \mathrm{~mm} \cdot 5000 \mathrm{~N}}{\pi \cdot 18_{\mathrm{mm}}} \\ \tau_{i}=157,19 \mathrm{MPa} \quad \tau_{i}=157,19 \mathrm{MPa}<t_{i 2 \mathrm{~L}}=650 \mathrm{MPa} \\ \tau_{i \text { mar }}=\frac{S_{\text {max }}}{S 1,0} \cdot \tau:=\frac{2222 \mathrm{~mm}}{12,22 \mathrm{~mm}} \cdot 157,19 \mathrm{MPa}=285,82 \mathrm{MPa} \end{array} \)
\( \begin{array}{l} s_{\text {max }}=s 1,0+\Delta_{s} \\ s_{1,5}=\frac{8 \cdot F \cdot D^{3} \cdot \text { if }}{G \cdot d^{4}}=\frac{8 \cdot 5000 \mathrm{~N} \cdot 72^{3} \mathrm{~mm}^{3} \cdot 7}{8,15 \cdot 10^{4} \mathrm{~N} / \mathrm{mm}^{2} \cdot 18_{\mathrm{mm}}^{4}} \\ s_{1,0}=12,22 \mathrm{~mm} \\ s_{\text {max }}=12,22 \mathrm{~mm}+10 \mathrm{~mm}=22,22 \mathrm{~mm} \end{array} \)
c)
\( C_{3}=C_{1}+C_{2}=202 \mathrm{~N} / \mathrm{mm}+150 \mathrm{~N} / \mathrm{mm}=352 \mathrm{~N} / \mathrm{mm} \)
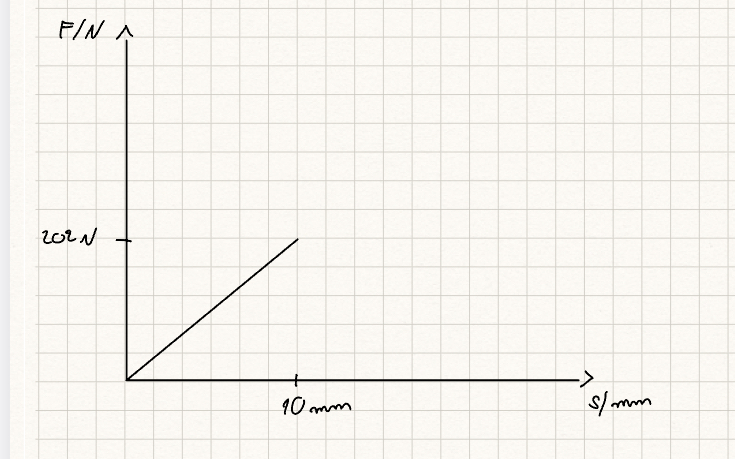
Hallo zusammen,
ich bin gerade an der Übungsaufgabe dran. Bin mir aber unsicher, wie ich die Federkennlinie zeichnen soll. Kann mir da jemand weiterhelfen?
Schönes Wochenende und schöne Grüße