Aufgabe:
Text erkannt:
Aufgabe 6: Auftrieb in Flüssigkeiten
Ein Körper, bestehend aus zwei Kuben, schwimmt auf dem Wasser.
\( \operatorname{Dim}[m] \)
Die Abmessungen der Kuben sind dem Bild zu entnehmen.
Die Kuben sind zentrisch angeordnet, so dass keine Schieflage eintritt.
Die Kuben haben unterschiedliche Werte der Dichte.
Wie tief \( h[\mathrm{~m}] \) taucht der obere Kubus ein?
\( \rho_{\text {wasser }}=1000 \mathrm{~kg} / \mathrm{m}_{3} \)
Erdbeschleunigung \( =9,81 \mathrm{~m} / \mathrm{s} 2 \)
Problem/Ansatz:
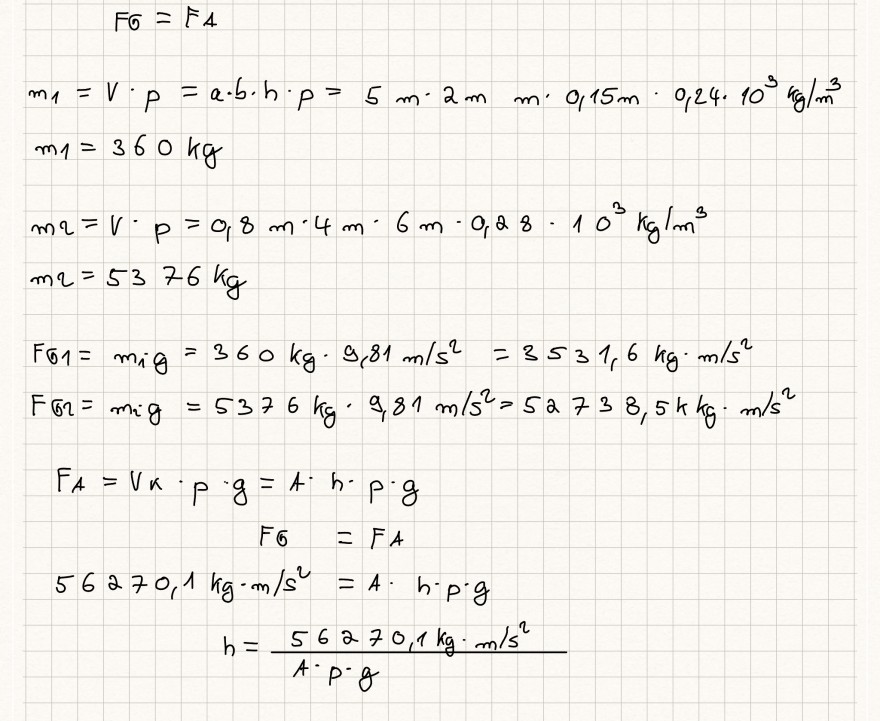
Text erkannt:
\( \begin{array}{l}F_{G}=F_{A} \\ m_{1}=V \cdot p=a \cdot b \cdot h \cdot p=5 \mathrm{~m} \cdot 2 \mathrm{~m} \mathrm{~m} \cdot 0,15 \mathrm{~m} \cdot 0,24 \cdot 10^{3} \mathrm{~kg} / \mathrm{m}^{3} \\ m_{1}=360 \mathrm{~kg} \\ m q=V \cdot p=0,8 \mathrm{~m} \cdot 4 \mathrm{~m} \cdot 6 \mathrm{~m} \cdot 0,28 \cdot 10^{3} \mathrm{~kg} / \mathrm{m}^{3} \\ m q=5376 \mathrm{~kg} \\ F \sigma_{1}=m_{i g}=360 \mathrm{~kg} \cdot 9,81 \mathrm{~m} / \mathrm{s}^{2}=3531,6 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2} \\ F_{\sigma_{2}}=m_{i} g=5376 \mathrm{~kg} \cdot 9,81 \mathrm{~m} / \mathrm{s}^{2}=52738,5 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2} \\ F_{A}=V_{K} \cdot p \cdot g=A \cdot h \cdot p \cdot g \\ F G=F A \\ 56270,1 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}=A \cdot h \cdot p \cdot g \\ h=\frac{56270,1 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}}{A \cdot P \cdot g} \\\end{array} \)
Hallo, ich habe diese Aufgabe bis an diesen Punkt gelöst. Jedoch weiß ich nicht, wie ich auf die Eintauchhöhe vom oberen Körper komme, weil ja 2 unterschiedliche Dichten gegeben sind.