Text erkannt:
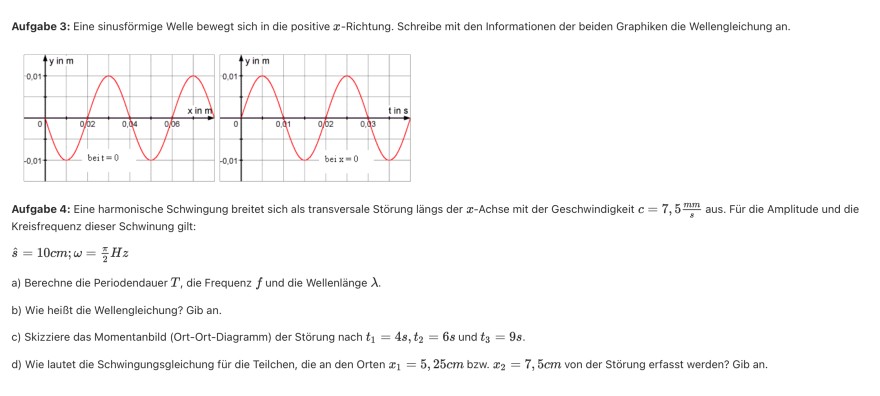
Aufgabe 3: Eine sinusförmige Welle bewegt sich in die positive \( x \)-Richtung. Schreibe mit den Informationen der beiden Graphiken die Wellengleichung an.
Aufgabe 4: Eine harmonische Schwingung breitet sich als transversale Störung längs der \( x \)-Achse mit der Geschwindigkeit \( c=7,5 \frac{m m}{s} \) aus. Für die Amplitude und die Kreisfrequenz dieser Schwinung gilt:
\( \hat{s}=10 \mathrm{~cm} ; \omega=\frac{\pi}{2} H z \)
a) Berechne die Periodendauer \( T \), die Frequenz \( f \) und die Wellenlänge \( \lambda \).
b) Wie heißt die Wellengleichung? Gib an.
c) Skizziere das Momentanbild (Ort-Ort-Diagramm) der Störung nach \( t_{1}=4 s, t_{2}=6 s \) und \( t_{3}=9 s \).
d) Wie lautet die Schwingungsgleichung für die Teilchen, die an den Orten \( x_{1}=5,25 \mathrm{~cm} \) bzw. \( x_{2}=7,5 \mathrm{~cm} \) von der Störung erfasst werden? Gib an.

Text erkannt:
Aufgabe 3: Entlang eines linearen Wellenträgers befinden sich 20 schwingungsfähige Massepunkte \( \left(m_{1}-m_{20}\right) \) im Abstand von je \( 1 \mathrm{~cm} \). Das Teilchen \( m_{1} \) am Ort \( x_{1}=0 \) werde zur Zeit \( t=0 \mathrm{~s} \) zu harmonischen Querschwingungen der Amplitude \( \hat{s}=2,5 \mathrm{~cm} \) angeregt. Nach \( 1,5 \mathrm{~s} \) ist \( m_{1} \) zum ersten mal maximal ausgelenkt und \( m_{4} \) beginnt gerade zu schwingen. Berechne Frequenz, Wellenlänge und Ausbreitungsgeschwindigkeit der Welle.
Aufgabe 4: Von einem Punkt am Ort \( x=0 \) breitet sich eine Transversalwelle in positiver \( x \)-Richtung mit der Geschwindigkeit \( c=3,2 \frac{\mathrm{m}}{\mathrm{s}} \) aus. Die Welle beginnt am Entstehungsort mit zunehmender positiver Elongation. Die Amplitude beträgt \( 20 \mathrm{~cm} \), die Frequenz \( f=0,6 \mathrm{~Hz} \).
a) Wie groß sind die Schwingungsdauer und die Wellenlänge dieser Welle?
b) Nach welcher Zeit hat die Welle den Ort \( x=2,25 m \) erreicht?
c) Gib eine Gleichung für die Welle an.
d) Welche Elongation hat ein Teilchen am Ort \( x=2,25 m \) nach \( 3,2 s \) ?

Text erkannt:
2. Wellen
2.19. Aufgaben zur Interferenzen
Aufgabe 1: Zur Bestimmung der Wellenlänge von Ultraschallwellen wird ein Interferenzversuch durchgeführt. Zwei als Sender benutzte Ultraschallwandler sind parallel an einen Sinusgenerator angeschlossen. Ihr Abstand beträgt \( 6 \mathrm{~cm} \). Auf einer \( 30 \mathrm{~cm} \) entfernten Geraden (parallel zur Verbindungslinie der beiden Sender werden mit Hilfe eines Empfängers Interferenzmaxima festgestellt. Der Abstand zwischen dem Maximum nullter und dem zweiter Ordnung beträgt \( 12 \mathrm{~cm} \).
Bestimme:
a) Welche Wellenlänge ergibt sich?
b) Mit welcher Frequenz schwingen die Lautsprechermembranen, wenn die Schallgeschwindigkeit \( 340 \mathrm{~m} / \mathrm{s} \) beträgt?

Text erkannt:
Aufgabe 2:
Zwei Schallstrahler \( S_{1} \) und \( S_{2} \) sind so an einen Tonfrequenzgenerator angeschlossen, dass sie stets mit gleicher Frequenz und in gleicher Phase schwingen. Der Abstand zwischen beiden Strahlern beträgt \( 1,00 \mathrm{~m} \). Ein Mikrofon ist \( 1,80 \mathrm{~m} \) von \( \mathrm{S}_{1} \) entfernt. Die Verbindungslinien bilden einen rechten Winkel:
a) Berechne den Gangunterschied der Strahler zum Mikrofon.
b) Die Frequenz am Generator wird auf \( f_{0}=3970 \mathrm{~Hz} \) eingestellt, so dass das Mikrofon ein Lautstärkemaximum registriert. Wie hängen Gangunterschied und Wellenlänge zusammen?
c) Man weiß, dass die Wellenlänge bei diesem Versuchsaufbau zwischen \( 8 \mathrm{~cm} \) und \( 9 \mathrm{~cm} \) beträgt. Wie ist der genaue Wert für die Wellenlänge?
d) Bei unverändertem Versuchsaufbau soll jetzt die Frequenz des Generators vergrößert bzw, verkleinert werden. Ermittle jeweils eine Frequenz, bei der das Mikrofon ein Lautstärkeminim registrieren würde.
Heyy, ich schreibe in Physik eine Arbeit und komme bei den Übungsaufgaben nicht voran.
Danke im Voraus!