Aufgabe:
Ich habe folgende Aufgabe zu einem Fadenpendel: Das mathematische Pendel ist ein schwingendes System (Annahme: Punktmasse an masseloser Stange, ohne Reibungs- verluste). Nehmen Sie an, dass Sie die explizite Lösung (1) der Bewegungsgleichung und damit auch (f) und die Periodendauer nicht kennen.
a. Mit welchem physikalischen Prinzip können Sie trotzdem die maximale Geschwin- digkeit des Pendels in einer Schwingungsperiode ermitteln, wenn das Pendel bei aus einer Ruhelage bei (0) losgelassen wurde?
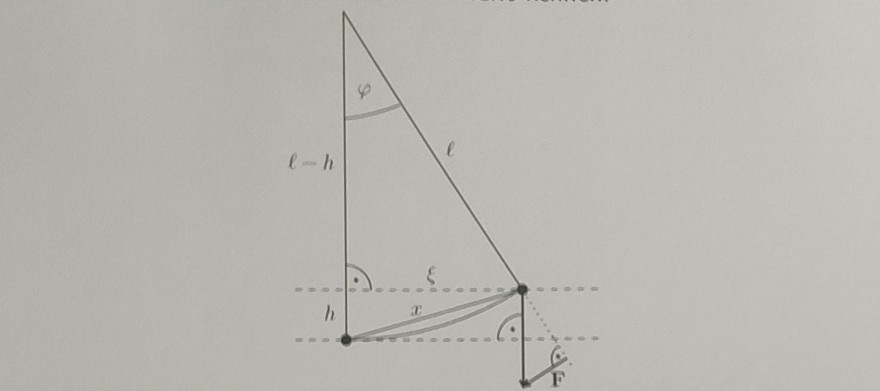
b. Berechnen Sie damit die maximale Geschwindigkeit für die Pendellänge l=2.5 m
und die Anfangsauslenkung x(0)= 0,7 m. Für den Auslenkungswinkel zu Beginn gelte<π/2. Hinweise: Rechnen Sie ohne Kleinwinkelnäherung. Verwenden Sie den Satz des Pythagoras. Die Erdbeschleunigung nähen Sie zu g = 10 m/s²
Problem/Ansatz:
a. Weiß ich wie ich machen soll. Ich kann da ja die Epot=Ekin stellen und nach v umformen.
v=√(2*g*h)
Aber wie kann ich b. Lösen vorallem mit dem satzt des Pythagoras? Für b. muss ich ja zunächst die höhe h berechnen.
Kann mir jemand den vollen Rechenwege für b. geben.