Aufgabe:
Folgende Aufgabe;
Die Lagerreaktionen sollten so gut wie richtig sein. Mir geht es um die Schnittgrössen. Ist bei denen mein Weg richtig?
Text erkannt:
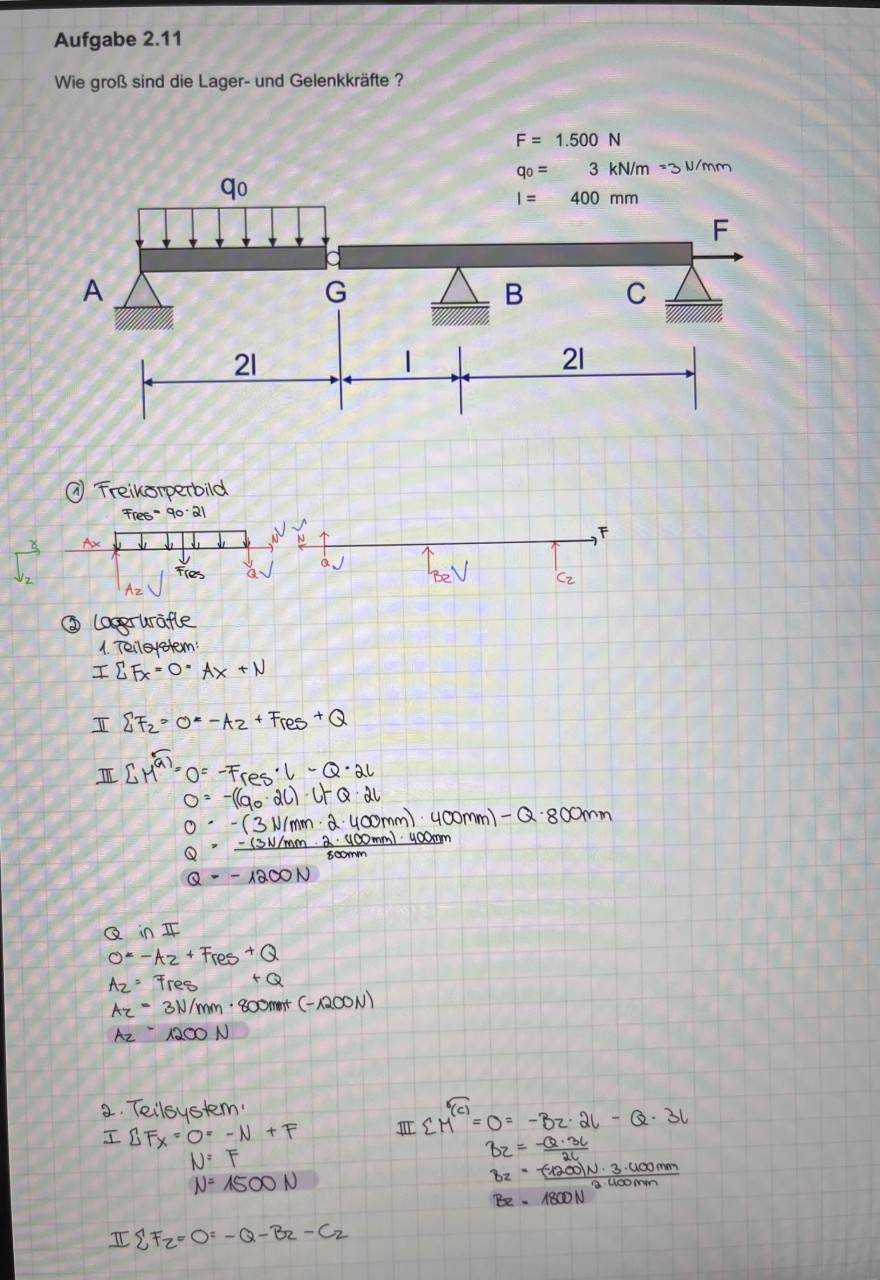
Aufgabe 2.11
Wie groß sind die Lager- und Gelenkkräfte ?
(1) Freikorpetbild
(2) Logeruräfle
1. Teiloystem:
\( \begin{array}{l} I \sum F_{x}=0 \cdot A x+N \\ \text { II } \Sigma F_{2}=0=-A_{2}+\text { Fres }+Q \\ \text { III } \Sigma M^{(a)}=0=-F_{\text {res }} \cdot l-Q \cdot 2 l \\ 0=-\left(\left(q_{0} \cdot 2 L\right) \cdot u+Q \cdot 2 L\right. \\ \text { O- }-(3 \mathrm{~N} / \mathrm{mm} \cdot 2 \cdot 400 \mathrm{~mm}) \cdot 400 \mathrm{~mm})-Q \cdot 800 \mathrm{~mm} \\ Q=\frac{-(3 \mathrm{~N} / \mathrm{mm} \cdot 2 \cdot 400 \mathrm{~mm}) \cdot 400 \mathrm{~mm}}{500 \mathrm{~mm}} \\ \text { Q }-1200 \mathrm{~N} \\ \end{array} \)
\( \begin{array}{l} Q \text { in II } \\ O=-A_{2}+\text { Fres }+Q \\ A_{2}=\text { Tres }+Q \\ A_{2}=3 \mathrm{~N} / \mathrm{mm} \cdot 800 \mathrm{~mm}+(-1200 \mathrm{~N}) \\ A_{2}=1200 \mathrm{~N} \end{array} \)
2. Teilsystem:
\( \begin{aligned} \text { I SFx }=0 & =-N+F \\ N & =F \\ N & =1500 \mathrm{~N} \end{aligned} \)
II \( \sum F_{2}=O=-Q-B_{2}-C_{2} \)
\( \text { III } \begin{aligned} E M^{(c)}= & =-B z \cdot 2 l-Q \cdot 3 l \\ & b z=-\frac{Q \cdot 3 l}{2 l} \\ & 8 z=\frac{-1200) \mathrm{N} \cdot 3 \cdot 400 \mathrm{~mm}}{2 \cdot 400 \mathrm{~mm}} \\ & B z=1800 \mathrm{~N} \end{aligned} \)

Text erkannt:
\( \mathrm{N} \) in I von 1.TS
\( \begin{array}{l} 0=A x+N \\ A_{x}=-N \\ A x=-1500 N \end{array} \)
\( \mathrm{Br} \) in II von 2.15
\( \begin{array}{l} O=-Q-B_{2}-C_{2} \\ C_{2}=-Q-B_{2} \\ C_{2}=-(-1200 \mathrm{~N})-1800 \mathrm{~N} \\ G_{2}=-600 \mathrm{~N} \end{array} \)
(3) Schnittrealutionen
1. Schnitt: \( 0 \leqslant x \leqslant 26 \)
2. Schnitt: \( 2 l \leq x \leq 32 \)
II \( \sum F_{2}=0=-A_{2}+ \) Fres \( N+V \)
\( V=A_{z} \)-Fres
\( V=1200 \mathrm{~N}-9_{0} \cdot x \)
\( V(x)=1200 \mathrm{~N}-3 \mathrm{~N} / \mathrm{mm} \cdot x \)
\( V(0)=1200 \mathrm{~N} \)
\( \begin{aligned} V(24) & =1200 \mathrm{~N}-3 \mathrm{~N}(\mathrm{~mm} \cdot 2 \cdot 400 \mathrm{~mm} \\ & =-1200 \mathrm{~N} \end{aligned} \)
\( \begin{aligned} \text { I } \sum F_{x}=0 & =-H \\ H & =0 \\ \text { II } \& F_{2}=0 & =-V-B_{2} \\ V & =-B_{2} \end{aligned} \)
\( \text { III } \begin{aligned} V & =-1800 \mathrm{~N} \\ M^{(x)}=0 & =-M_{b}+B z \cdot(36-x) \end{aligned} \)
\( \begin{array}{l} M b(x)=B z \cdot(3 l-x) \\ M b(x)=1800 \mathrm{~N} \cdot(3 \cdot 400 \mathrm{~mm}-x) \\ M b(2 l)=720000 \mathrm{~N} / \mathrm{mm} \end{array} \)
\( \mathrm{Mb}(3 \mathrm{l})=0 \)
\( \text { III } \begin{aligned} M^{(x)}=0 & =-M_{b}-\operatorname{Tresn} \cdot \frac{x}{2}+A_{2} \cdot x \\ M b(x) & =- \text { Fresn } \cdot \frac{x}{2}+A_{2} \cdot x \\ M b(x) & =-\left(3 N /(m n \cdot x) \cdot \frac{x}{2}+1200 N \cdot x\right. \\ M b(0) & =0 \\ M b(2 L) & =0 \end{aligned} \)
3. schnitt: \( 3 l \leq x \leq 54 \)
\( \begin{array}{l} \text { II } \sum \dot{M}^{(x)}=0=-M b+G \cdot(5 l-x) \\ M b(x)=C_{2} \cdot(51-x) \\ M b(x)=-600 \mathrm{~N} \cdot(5 \cdot 400 \mathrm{~mm}-x) \\ \mathrm{Mb}(3)=-480000 \mathrm{~N} \\ \end{array} \)
\( \operatorname{Mo}(5 l)=0 \)