Text erkannt:
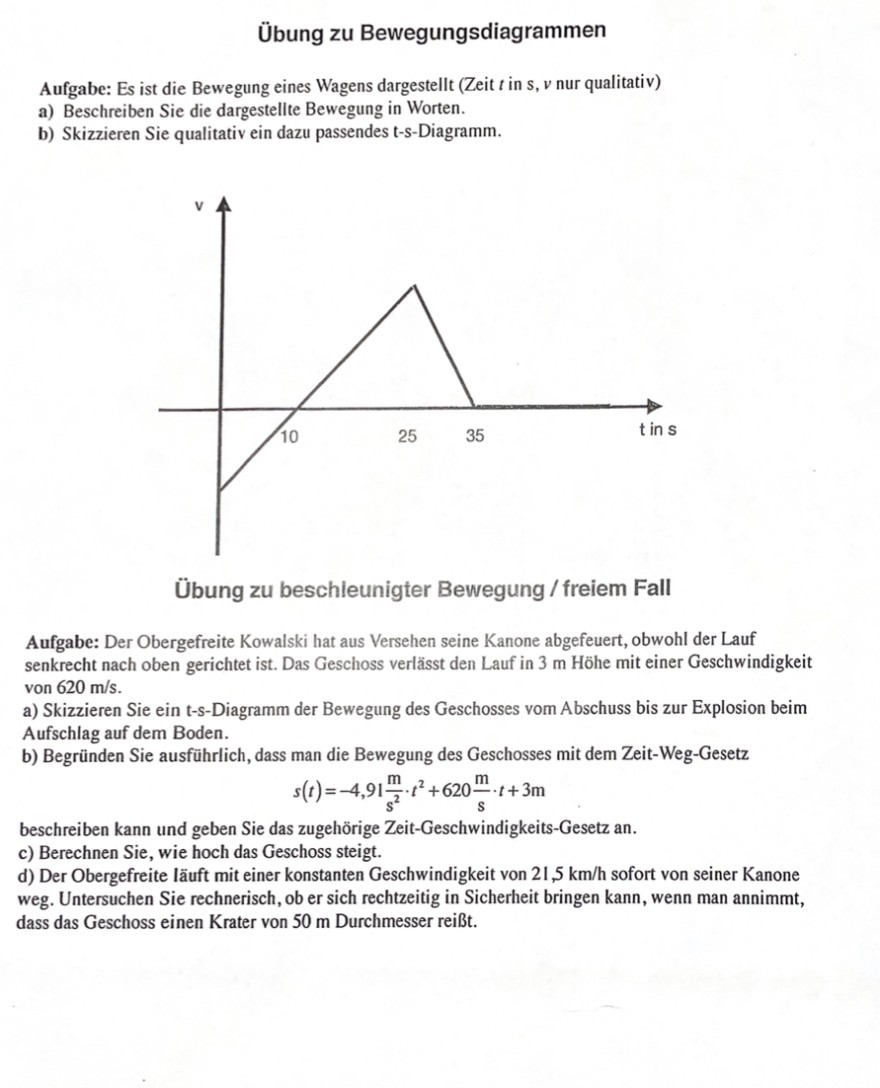
Übung zu Bewegungsdiagrammen
Aufgabe: Es ist die Bewegung eines Wagens dargestellt (Zeit \( t \) in \( s, v \) nur qualitativ)
a) Beschreiben Sie die dargestellte Bewegung in Worten.
b) Skizzieren Sie qualitativ ein dazu passendes t-s-Diagramm.
Übung zu beschleunigter Bewegung / freiem Fall
Aufgabe: Der Obergefreite Kowalski hat aus Versehen seine Kanone abgefeuert, obwohl der Lauf senkrecht nach oben gerichtet ist. Das Geschoss verlässt den Lauf in \( 3 \mathrm{~m} \) Höhe mit einer Geschwindigkeit von \( 620 \mathrm{~m} / \mathrm{s} \).
a) Skizzieren Sie ein t-s-Diagramm der Bewegung des Geschosses vom Abschuss bis zur Explosion beim Aufschlag auf dem Boden.
b) Begründen Sie ausführlich, dass man die Bewegung des Geschosses mit dem Zeit-Weg-Gesetz
\( s(t)=-4,91 \frac{\mathrm{m}}{\mathrm{s}^{2}} \cdot t^{2}+620 \frac{\mathrm{m}}{\mathrm{s}} \cdot t+3 \mathrm{~m} \)
beschreiben kann und geben Sie das zugehörige Zeit-Geschwindigkeits-Gesetz an.
c) Berechnen Sie, wie hoch das Geschoss steigt.
d) Der Obergefreite läuft mit einer konstanten Geschwindigkeit von \( 21,5 \mathrm{~km} / \mathrm{h} \) sofort von seiner Kanone weg. Untersuchen Sie rechnerisch, ob er sich rechtzeitig in Sicherheit bringen kann, wenn man annimmt, dass das Geschoss einen Krater von \( 50 \mathrm{~m} \) Durchmesser reißt.
Aufgabe: