Aufgabe:Hallo zusammen, habe folgende Aufgabe: Ein Körper mit der Masse 20 kg soll in 1s bei gleichmäßiger Beschleunigung 80 cm hochgezogen werden.
Welche Kraft ist dazu erforderlich?
Welche Endgeschwindigkeit erreicht der Körper?
Problem/Ansatz: wollte die zweite Aufgabe mit dem Energieerhaltungssatz rechnen, bekomme dort, aber ein anderes Ergebnis als mit der normalen raus. Hoffe mir kann jemand helfen. Danke im vorrau.
LG Lena

Text erkannt:
ÜSer Energierhattung:
\( \begin{array}{l} W_{2}=\underbrace{m \cdot g \cdot h}_{156,96 \mathrm{Nm}}+\underbrace{\frac{1}{2} m v^{2}}_{\substack{25,67 \\ \left(\frac{1}{2} \cdot 20 \cdot 1,6^{2}\right)}} \\ 0,8 m \sqrt{\square} W_{1}=0 \\ 0=m \cdot g \cdot h+\frac{1}{2} v^{2} \\ \text { Warum } \\ m \cdot g \cdot h=\frac{1}{2} m \cdot v^{2} \\ \text { anderes } \\ \text { TEgesnis? } \\ V=\sqrt{\frac{2 p \cdot g \cdot h}{m}}=\sqrt{2 \cdot 9,81 \cdot 0,8}=3,96 \frac{\mathrm{m}}{\mathrm{s}} \\ \end{array} \)
Text erkannt:
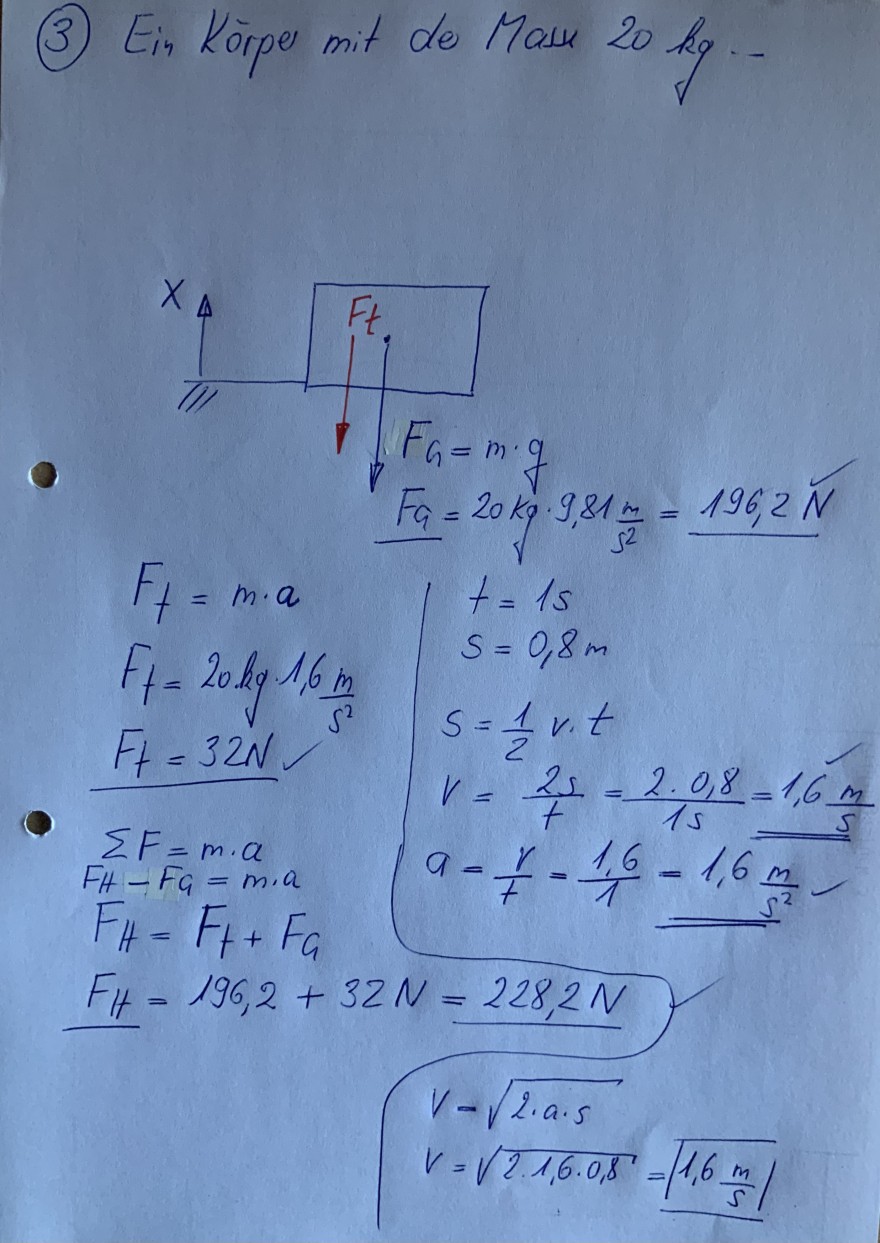
(3) Ein Korper mit de Masu \( 20 \mathrm{~kg} \)..
\( \begin{array}{l} F_{H}=F_{t}+F_{G} \\ F_{H}=196,2+32 \mathrm{~N}=228,2 \mathrm{~N} \\ V-\sqrt{2 \cdot a \cdot 5} \\ V=\sqrt{2 \cdot 1,6 \cdot 0,8}=1,6 \frac{\mathrm{m}}{\mathrm{s}} \\ \end{array} \)