Aufgabe:
Hallo
habe eine Frage zur gekoppelten Federschwingung.
(Siehe Bild)
Problem/Ansatz:
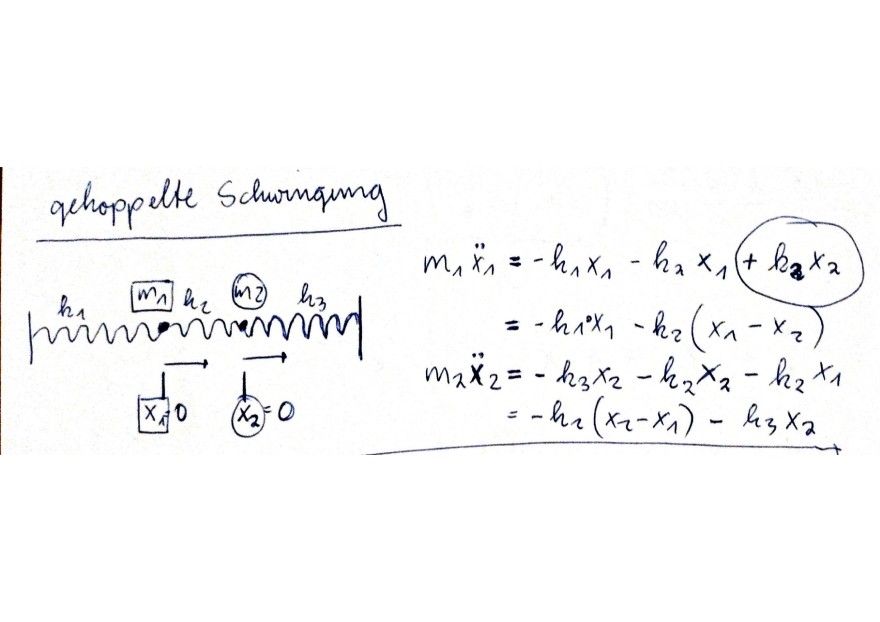
Warum entsteht der postive Term? (Ist im Bild umrundet)
Text erkannt:
qehoppelte Schwinqung
prirvonvarvon
\( \begin{aligned} m_{1} \ddot{x}_{1} & =-h_{1} x_{1}-h_{2} x_{1}+k_{2} x_{2} \\ & =-h_{1} x_{1}-h_{2}\left(x_{1}-x_{2}\right) \\ m_{2} \ddot{x}_{2} & =-h_{3} x_{2}-h_{2} x_{2}-h_{2} x_{1} \\ & =-h_{2}\left(x_{2}-x_{1}\right)-h_{3} x_{2} \end{aligned} \)
Wenn man die Masse m2 nach rechts verschiebt, dann kommt m1 auch nach rechts.
Das ist relativ klar. Aber wenn man dann m2 loslässt dann wirkt die rücktreibende Kraft doch wieder und der Term sollte negativ sein??
LG