Aufgabe:
1. Eine ruhende Kugel mit der Masse m = 10 kg wird aus einer Höhe von h1 = 10 m durch die Gravitation konstant mit g = 9.81 m/s² beschleunigt und schlägt auf der Höhe h2 = 0 m in den Boden ein.
2. Eine ruhende Probeladung qe = 1.6 × 1019 As wird in einem homogenen elektrischen Feld E = 10 kV/m von x1 = 0 cm bis x2 = 30 cm beschleunigt. Der Einfluss der Gravitationskraft auf die Probeladung sei zu vernachlässigen.
a) Berechnen Sie für 1. und 2. die potentielle Energie in Startposition, nach 30 % und nach 50 % der maximal hinterlegbaren Strecke. Geben Sie zusätzlich die zugehörige kinetische Energie in jeder Position an. Welcher Zusammenhang lässt sich zwischen potentieller und kinetischer Energie erkennen?
b) Die ruhende Probeladung wird jetzt in einem elektrischen Feld E(x) = 10 * 1/x * ln(x) von x1 = 1 m bis x2 = 10 m beschleunigt. Berechnen Sie die potentielle Energie in Startposition, nach 30 % und nach 50 % der maximal hinterlegbaren Strecke. Welcher Unterschied bezüglich potentieller und kinetischer Energie fällt Ihnen im Vergleich zu a) auf? Zur Lösung des Integrals dürfen Sie die Beziehung ∫ f'(x) * f(x) = 1/2 f (x)² verwenden. Setzen Sie in E(x) für die x-Werte ausschließlich die Zahlenwerte (ohne die Einheit Meter) ein, damit Sie auf die richtige Einheit kommen
Problem/Ansatz:
a) für 1.) Startpostion Epot = = m * g * h1 = 10kg * 9,81 m/s² * 10 m = 981 J.
E_kin = 0
nach 30 %: E_pot_30 = m* g * (h1 *0,30) = 10 kg * 9,81 m/s² * 7m = 686,7 J
E_kin_30 = E_pot - E_pot_30 = 981 J - 686, J = 294, 3 J
nach 50 %: E_pot_50 = m * g * (h1 * 0,5) = 10 kg * 9,81 m/s² * 5m = 450 J
E_kin_50 = E_pot - E_pot_50 = 981 J - 490,5 J = 490, 5 J
für 2). Startpositon : E_pot = qe * E * x1 = 1,6 * 10^-19 As * 10 kV/m * 0 cm = 0 J
E_kin = 0 J
nach 30 %: E_pot_30 = qe * E * (x2*0,3) = 1,6 * 10^-19 As * 10 kV/m * 9 cm = 1,44 * 10^-17 J
E_kin_30 = E_pot_30 - E_pot = 1,44 * 10^-17 J - 0 J = 1,44 * 10^-17 J
nach 50 %: E_pot_50 = qe * E * (x2*0,5) = 1,6 * 10^-19 As * 10 kV/m * 15 cm = 2,4 * 10^-17 J
E_kin_50 = E_pot_50 - E_pot = 2,4 * 10^-17 J - 0 J = 2,4 * 10^-17 J
b) Da hab ich im Skript folgende Formel gefunden:
Δ Ep = - ∫(von r1 nach r2) F * dr = -q ∫(von r1 nach r2) E * dr
Eingesetzt mit unseren Werten wäre das:
Ep = -qe ∫(von x1 nach x2) 10 * 1/x ln (x)
So, jetzt machen wir uns die Beziehung ∫ f'(x) * f(x) = 1/2 f (x)² zu nutze, um den Übungsleiter glücklich zu machen. Dann kommen wir auf:
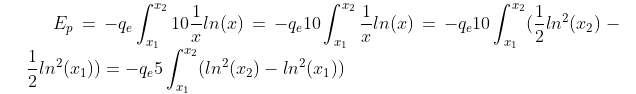
Text erkannt:
\( \begin{array}{c}E_{p}=-q_{e} \int \limits_{x_{1}}^{x_{2}} 10 \frac{1}{x} \ln (x)=-q_{e} 10 \int \limits_{x_{1}}^{x_{2}} \frac{1}{x} \ln (x)=-q_{e} 10 \int \limits_{x_{1}}^{x_{2}}\left(\frac{1}{2} \ln ^{2}\left(x_{2}\right)-\right. \\ \left.\frac{1}{2} \ln ^{2}\left(x_{1}\right)\right)=-q_{e} 5 \int \limits_{x_{1}}^{x_{2}}\left(\ln ^{2}\left(x_{2}\right)-\ln ^{2}\left(x_{1}\right)\right)\end{array} \)
So und ab jetzt geht die Action los! Denn wenn ich jetzt versuche diesen Ausdruck zur Berechnung der potenziellen Energie zu nutzen komm ich nicht weiter.
Für die Startpositon E_pot_Start hätte ich: -qe * 5 * (ln²(x2) - 1/2 ln²(x1)). Erstmal ist mir nicht ganz klar, was ich genau für x1 und x2 einsetzen soll. Ich habe jetzt beides Mal die 1 genommen, weil wir ja in der Startpostion sind. Kommt man auf: -1,6 * 10^-19 * 5 (ln²(1) - lin²(1)) = 0
Jetzt zu der potenziellen Energie nach 30 %. Ich hab mir überlegt, dass ich da die Werte x1 = 1 cm und für x2 , da wir 30 % der Strecke überwunden haben x2 = 10 cm * 0, 3 = 3 cm einsetze.
Kommt man auf -1,6 * 1019 * 5 (ln²(3) - ln²(1)) = -9,65 * 1019.
Für die potenzielle Energie nach 50 % diesselbe Überlegung, nur für x1 = 1cm und x2 = 5 cm: => -1,6 * 10^-19 * 5 (ln²(5) - ln²(1)) = -2,07*10-18
Und somit ist die potenzielle Energie nach 50 % der Strecke kleiner als nach 30 % der Strecke. Und das kann nicht sein. Kann mir jemand bitte kurz sagen, wo mein Fehler liegt.
Außerdem braucht man um zu erklären welcher Unterschied auffält noch die kentische Energie. Da hab ich jetzt die Formel E_kin = 1/2 * m * v². Aber E_kin und v² sind doch gar nicht bekannt? Soll man bei 30 % E_pot + E_kin = E_pot_30 + E_kin_30 nehmen und dann nach v² auflösen. Da wir bei Start v1 = 0 ist wäme man dann auf 0 + 1/2 m * v12 = m * g * 0,3 * 1/2 mv22. Aufgelöst nach v2 =√2*g*x2 *30 % ) = √2* 9,81 * 3m = 7,6720 und dann eingesetzt in die Formel für die kinetische Energie Ekin = 1/2 m v22 = 1/2 * 10 kg * (7,6720 m/s )². = 294, 2979 J.
Und für 50 % dann dasselbe nur mit 50 % statt 30 % also v2 =√2*g*x2 *50 % ) = √2* 9,81 * 3m = 9,9045 J und dann Ekin = 1/2 m v22 = 1/2 * 10 kg * (9,9045 m/s )². = 490,4956 J. Kann das sein?
Also am meisten verwirrt mich das mit der potenziellen Energie in Aufgabe b). Das muss ich irgendwas falsch gemacht haben.
Liebe Grüße,
Marceline The Vampire Queen