Aufgabe:
Wie muss man ein langsam abrollendes und lange schwingendes Maxwellrad konstruieren?
Problem/Ansatz:
Wir haben diese Formel.
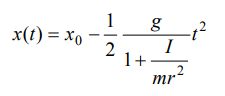
Text erkannt:
\( x(t)=x_{0}-\frac{1}{2} \frac{g}{1+\frac{I}{m r^{2}}} t^{2} \)
Gefragt ist ja, dass x0-x(t) bei derselben Zeit möglichst klein bleibt. Dafür muss man entweder das Trägheitsmoment senken oder m*r^2 erhöhen. Aber da I=1/2 m*r^2 ist, widerspricht sich das ja, bzw. es ist egal, was man an m oder r ändert. Was gibt es denn dann für Möglichkeiten?
Und beim zweiten Teil der Frage möchte man ja den Energieverlust möglichst minimieren? Wie macht man das am besten?
Schonmal danke für die Hilfe!