Entfernungsabhängige Interferenz zweier Schallwellen

Question

Aufgabe:

In der Abbildung ist die Situation von zwei punktförmigen
Schallquellen S₁ und S₂ zu sehen, die beide Kugelwellen der
gleichen Phasenlage aussenden.

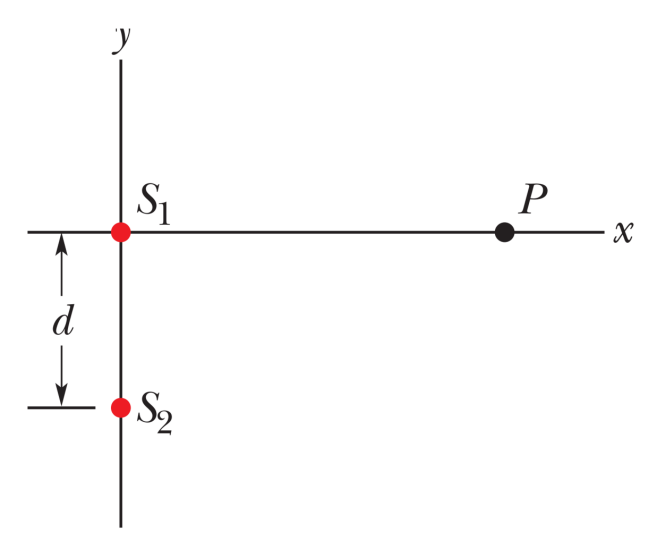
Die Wellenlänge der Schallsignale sind 2,00 m. Der Abstand der beiden Schallquellen beträgt

16,0 m.

a)

Wie groß ist Phasendifferenz zwischen den beiden emittierten Wellen, wenn der Punkt P unendlichen weit von S₁
entfernt ist und welche Art von Interferenz liegt dann vor?

b)

Wie verändert sich Phasendifferenz zwischen den beiden emittierten Wellen am Punkt P, wenn
dieser vom Unendlichen in Richtung S₁ bewegt wird (Leitet bitte eine Formel ab)?

c)

Bei welchem Abstand des Punktes P zur Quelle S₁ ist die Phasendifferenz 0.5 λ, 1.0 λ und 1.5 λ?

Problem/Ansatz:

a)

Die Aufgabenstellung ist meiner Meinung nach etwas ungenau formuliert, da kein Bezugspunkt für die Phasendifferenz angegeben wird. "Phasendifferenz" in Bezug auf welchen Punkt, bzw. in Bezug auf welche Wegstrecken, die von den beiden Wellenzügen zurückgelegt werden? Dem Kontext (und dem nachfolgenden Aufgabenteil) kann man zumindest entnehmen, dass wohl die Interferenz im Punkt P gemeint sein muss.

Idee: Formel für die Phasendifferenz (im Bogenmaß) anwenden:

\( \Delta \varphi = \frac{\Delta s}{\lambda} \cdot 2 \pi  \) 

Dabei gilt für den Wegunterschied \( \Delta s \):

\( \Delta s = \sqrt{d^2 + x^2} - x \), wobei x laut Abb. den Abstand zwischen S₁ und P beschreibt. Dann kann man den Limes dieser Gleichung von x gegen Unendlich bilden und kommt auf 0. Die Phasendifferenz nähert sich damit ebenfalls der 0 an und es kommt folglich zu konstruktiver Interferenz im Punkt P. Ist das so richtig?

b)

Hierzu habe ich keinen wirklichen Ansatz. Vielleicht kann man die beiden obigen Gleichungen kombinieren und kommt so auf eine allgemeine Formel für die Phasendifferenz (deren Angabe sich vermutlich auch in a) schon gelohnt hätte):

\( \Delta \varphi = \frac{\sqrt{d^2 + x^2} - x}{\lambda} \cdot 2 \pi  \)

In Abhängigkeit von der Veränderung des Abstandes x, also \( \Delta x \), könnte man nun also angeben:

\( \Delta \Delta \varphi = \frac{\sqrt{d^2 + (\Delta x)^2} - \Delta x}{\lambda} \cdot 2 \pi \)

Jedoch wirkt diese Gleichung unhandlich und ich bin mir nicht sicher, ob \( \Delta x \) so ohne weiteres eingesetzt werden darf.

c)

Ansatz: Hier kann man \( \Delta s \) nach x umstellen, also

\( x = \frac{d^2 - (\Delta s)^2}{2 \cdot \Delta s} \).

Dann kann man jeweils die in der Aufgabenstellung angegebenen Phasendifferenzen mit Hilfe der Angabe \( \lambda = 2,00 \, m \) in ein \( \Delta s \) umrechnen und in die Formel einsetzen, da d ebenfalls angegeben ist.

Answer 1

Hallo

Die Frage nach P in oo  hast du richtig, sie ist wirklich seltsam, denn da ist die Intensität einer Kugelwelle 0 also hilft positive Interferenz nichts. dass die Entfernung von S1 und S2 nach oo gleich ist, muss man nicht nachrechnen.

zu b) dabei ist wohl einfach statt x=oo  x einzusetzen  also dein

$$\Delta s=\sqrt{d^2+x^2}$$ was du da noch mit -x machst verstehe ich nicht, vielleicht dazu sagen x ist Abstand S1P oder nenne den Abstand statt x  xp.

c) eigentlich ist ein Phasenunterschied 2π ,π  und nicht der Wegunterschied

eine Wegunterschied von λ ergibt einen Phasenunterschied von 0 oder 2π usw.  Gefragt ist also nach dem Wegunterschied.

das ist einfach √(d^2-x_P^2)

stammt sie Aufgabe aus der Schule?

Gruß lul