Berechnen Sie die Spannung der Kapazität C1, die diese 10,75 ms nach dem Schließen des Schalters besitzt.

Question

Aufgabe:

In der nachfolgenden Schaltung beträgt die Quellspannung U=10 V und die Kapazitäten betragen C1=6 yF und C2=8 yF. Der Widerstand R1 beträgt 500 Ohm und der Widerstand R2 ist unbekannt. 10,75 ms nachdem der Schalter S geschlossen wurde, ist die Kapazität C1 zu 90% aufgeladen.

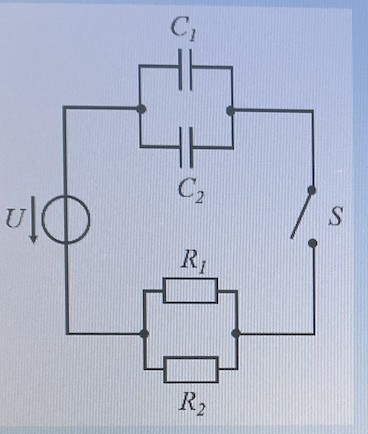
a) Skizzieren Sie eine vereinfachte Ersatzschaltung und geben Sie die Werte der Quellspannung und der Ersatzkapazität an.
b) Berechnen Sie die Spannung der Kapazität C1, die diese 10,75 ms nach dem Schließen des Schalters besitzt.
c) Berechnen Sie die Zeitkonstanten für die Aufladung der Kapazität C1 und die Aufladung der Kapazität C2.
d) Berechnen Sie den Widerstand R2.
e) Stellen Sie den zeitabhängigen Spannungsverlauf am Widerstand R2 graphisch dar

Problem/Ansatz:

Hallo, hier habe ich eine Aufgabe aus einer Altklausur die ich von einem Kommilitonen bekommen habe.

Leider komme ich bereits bei der b) nicht weiter, da meiner Meinung nach ein Strom gegeben sein muss, damit ich die abfallende Spannung über U_R1 = U_R2 berechnen kann, um wiederum die Spannung am Kondensator berechnen zu können.

Über Lösungsansätze würde ich mich freuen :-)

Mit freundlichen Grüßen

Answer 1

in der Aufgabe steht:

"10,75 ms nachdem der Schalter S geschlossen wurde, ist die Kapazität C1 zu 90% aufgeladen."

Wenn man unendlich lange wartet, ist die Kapazität auf die Quellspannung aufgeladen, also voll. 90% davon sind 9V

Die Zeitkonstante tau = Rges*Cges bekommst du aus

t= 10,75 ms

U(t) = 10V (1-e^(-t/tau)) =9V

Comments

Danke für deine Antwort, ich hätte aber da nicht zwei Fragen zu.

1.Warum können die Kondensatoren sich bis auf 10V aufladen?

Ich weiss nicht ob es ein Denkfehler ist aber wenn über die Widerstände eine Spannung abfällt und das Potential nach den Widerständen geringer ist, wie ist es möglich dass Kondensatoren sich auf die Ausgangsspannung aufladen können?

Als Bsp. sagen wir mal über den Widerstand Rges fallen 3V ab, so hat das Spannungspotential nach dem Widerstand nur noch 7V. Müsste dann nicht auch Kondensatorspannung auf diese 7V begrenzt sein?

2. Du sagst die Zeitkonstante tau erhalte ich aus Rges*Cges aber Rges kann ich ja nicht berechnen da mir der Widerstand R2 fehlt und die Formel zum aufladen eines Kondensator kann ich nicht nach tau umstellen da mir ja Uc fehlt.

---

1. Über die Widerstände fällt nur eine Spannung ab, wenn auch ein Strom durch sie fließt. Je mehr die Kondensatoren aufgeladen werden, desto kleiner wird der Unterschied zwischen der Spannung U und der Spannung an den Kondensatoren. Also wird auch die Spannung über den Widerständen immer kleiner und der Strom durch die Widerstände wird immer kleiner, und kleiner ,,, Eigentlich hört das nie auf, die Kondensatoren werden erst in unendlich langer Zeit wirklich auf U aufgeladen sein. Aber nach ca 7 tau unterscheidet sich die Spannung nur noch um weniger als 10mV von den 10V und der Strom ist auch nur noch < 1/1000 seines Anfangswertes.

2. Nein, ich sage nicht, dass man tau aus R und C ausrechen kann, solange man die noch nicht kennt. Umgekehrt wird ein Schuh draus: aus tau kann man R ausrechnen

Du must die Gleichung U(t) = U (1-e^(-t/tau)) nach tau auflösen

 1  -  U(t) /U =  e^(-t/tau)

-t/tau = ln (1-U(t)/U)

tau = -t/ ln (1-U(t)/U) =  -10,75 ms / ln(0.1) =  4.66 ms

Damit kannst du den Widerstand ausrechnen