Hallo,
hier die Berechnung der Transistorschaltung.
a) Berechnung für \(\large R_{L} -> \infty\):
Aus der Kennlinie kann man direkt ablesen
\(\large U_{Z} = 8V\)
\(\large U_{R1} = U_{S} - U_{Z}\)
\(\large U_{R1} = 7V\)
\(\large U_{R2} = U_{Z} - U_{BE}\)
\(\large U_{R2} = 7,17V\)
\(\large I_{R1} = \frac{U_{S} - U_{Z}}{R_{1}} = 40mA\)
Berchnung von \(\large I_{R2}\)
\(\large I_{R2} = \frac{U_{R2}}{R_{2}} = \frac{7,17V}{1378,8Ω}\)
\(\large I_{R2} = 5,2mA\)
Berechnung von \(\large I_{B}\)
aus \(\large I_{R2} = I_{B} + I_{C} = (B+1)*I_{B}\)
\(\large I_{B} = \frac{I_{R2}}{B + 1} = 56,52µA\)
b) wie klein darf \(\large R_{L}\) werden, bevor die Schaltung nicht mehr funktioniert
Für die Minimalstromstärke \(\large I_{Z,min}\) gilt
\(\large I_{Z,min} \approx \frac{I_{Z,max}}{15*\log_{}{U_{Z}}}\)
\(\large I_{Z,min} = 3,69mA\)
unterhalb von \(\large I_{Z,min}\) verliert die Z-Diode ihre Funktion
Durch Verkleinern des Lastwiderstandes \(\large R_{L}\) wird die Basis-Emitterspannung geringfügig erhöht, was einen starken Anstieg es Emitterstroms und damit einen größeren Basisstrom zur Folge hat. Somit wird auch der statische Basis-Emitterwiderstand kleiner. Der statische Basis-Emitterwiderstand ist der Gleichstromwiderstand \(\large \frac{U_{BE}}{I_{B}}\) und darf nicht mit dem Differenziellen Basis-Emitterwiderstand verwechselt werden!!
Betrachtet man \(\large R_{1}\) mit \(\large R_{BE}\), \(\large R_{2}\) und \(\large R_{L}\) als Spannungsteiler, so lässt sich folgendes Ersatzschaltbild zeichnen:
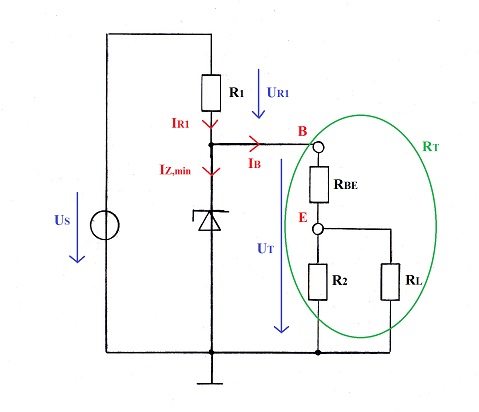
Wird durch Verkleinern von \(\large R_{L}\) der Gesamtwiderstand \(\large R_{T}\) so klein, dass die Teilspannung \(\large U_{T}\) kleiner wird als die Spannung \(\large U_{Z}\) , dann geht die Stabilisierungsfunktion der Z-Diode verloren und die Schaltung funktioniert nicht mehr. Dieser kritische Punkt liegt im Knickbereich der Z-Diode bei \(\large I_{Z,min}\).
Normalerweise wird \(\large I_{Z,min}\) nach folgender Gleichung berechnet:
\(\large I_{Z,min} \approx \frac{I_{Z,max}}{15*\log_{}{U_{Z}}}\)
Mit \(\large I_{Z,max} = 50mA\) und \(\large U_{Z} = 8V\) wird
\(\large I_{Z,min} = 3,69mA\)
\(\large I_{B} = I_{R1} - I_{Z,min} = 36,31mA\)
\(\large I_{E} = (B+1)*I_{B} = 92 * 36,31mA = 3340,43mA\)
\(\large I_{RL} = I_{E} - I_{R2} = 334043mA - 5,2mA\)
\(\large I_{RL} = 3335,225mA\)
\(\large R_{L} = \frac{7,17V}{3335,225mA}\)
\(\large R_{L} = 2,15Ω\)
\(\large R_{L}\) darf also nich kleiner als \(\large 2,15Ω\) werden, sonst funktioniert die Schaltung nicht mehr.
Gruß von hightech