Berechnen Sie den Austrittswinkel \alpha des Lichtstrahls.

Question

Guten Morgen Leute,

würde mich sehr freuen, falls mir jemand bei der folgenden Aufgabe weiterhelfen kann.

Mit freundlichen Grüßen

Ümit

Fragestellung: wie kommt man auf die „140 Grad“?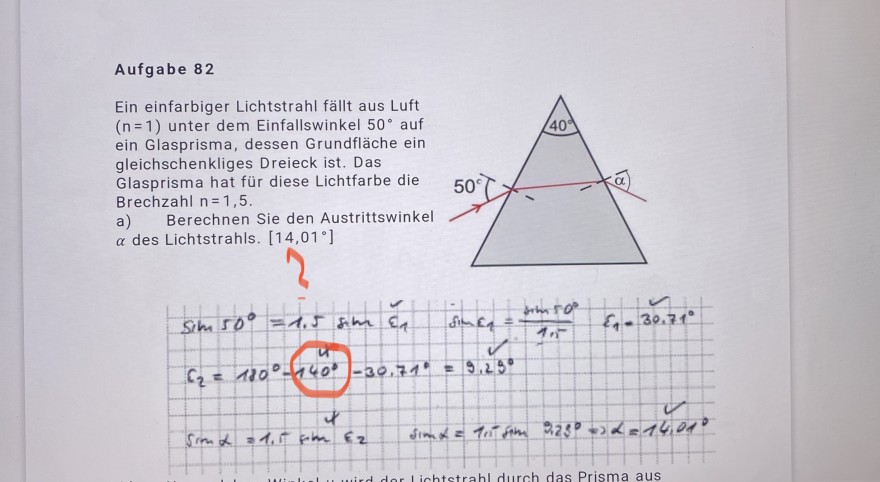

Text erkannt:

Aufgabe 82
Ein einfarbiger Lichtstrahl fällt aus Luft \( (n=1) \) unter dem Einfallswinkel \( 50^{\circ} \) auf ein Glasprisma, dessen Grundfläche ein gleichschenkliges Dreieck ist. Das
Glasprisma hat für diese Lichtfarbe die Brechzahl n=1,5.
a) Berechnen Sie den Austrittswinkel \( \alpha \) des Lichtstrahls. \( \left[14,01^{\circ}\right] \)
\( \sin 50^{\circ}=1.5 \mathrm{sm} \varepsilon_{1} \quad \sin c_{1}= \) \( C_{2}=180^{\circ}-140^{\circ}-30.71^{\circ}=9.29^{\circ} \)
\( \sin \alpha=1, r^{*} \mathrm{Fin} \varepsilon_{2} \quad \sin \alpha=11^{-} \sin \quad 323^{\circ} \Rightarrow \alpha=140^{\circ} \)

Answer 1

Hallo,

wie kommt man auf die „140 Grad“?

das obere (kleine) Dreieck mit der rot eingezeichneten Linie als Grundseite hat die folgenden Innenwinkel : 40° in der Spitze, 90°- ε₁ als linker Innenwinkel und 90°- ε₂ als rechter Innenwinkel. Weil die Winkelsumme im Dreieck 180° ist, folgt daraus:

40° + (90° - ε₁) + (90°- ε₂) = 180° | -40°

(90° - ε₁) + (90°- ε₂ ) = 140°

180° - ε₁ - ε₂ =  140°

ε₂ = 180° - 140° - ε₁

Gruß Enano

Comments

Vielen Dank. Hat mir sehr geholfen.