Zentripetalkraft und Gravitationskraft

Question

Aufgabe:

Hinweis: Die Aufgaben a) und b) sind voneinander unabhängig.

a) Die Internationale Raumstation ISS hat die Masse 4.3∙10⁵ [kg] und umkreist die Erde (Figur 4) in der Höhe h = 4.1∙10² [km].
In dieser Höhe berechnet sich die Gewichtskraft F_G eines Körpers durch F_G = m∙g, wobei g = 8.7 [m/s²].

a1) Berechnen Sie die Grösse der Gewichtskraft F_G der ISS und und zeichnen Sie F_G in Figur 4 gut sichtbar ein, beschriftet mit F_G (beachten Sie den Angriffspunkt).

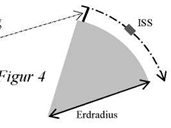
a2) Welche ist die Gegenkraft F von F_G? Beschreiben Sie F in Worten und zeichnen Sie F in Figur 4 ein, beschriftet mit F (beachten Sie den Angriffspunkt).

a3) Damit die ISS sich um die Erde bewegen kann, muss eine Zentripetalkraft wirken.

a31) Welche Kraft liefert die Zentripetalkraft? Begründen Sie Ihre Antwort.

a32) Wie gross ist die Zentripetalkraft (formal und numerisch)?

a4) Aus den obigen Überlegungen lässt sich die Geschwindigkeit der ISS bestimmen. Berechnen Sie die Geschwindigkeit (formal und numerisch, aber auch verbal begründen).

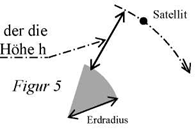
b) Berechnen Sie mit dem Gravitationsgesetz die Kraft, mit der die Erde einen anderen Satelliten anzieht, der die Erde in einer Höhe von 3.6∙10⁴ [km] umkreist und die Masse 1.2 [t] hat (Figur 5).

Text erkannt:

der die
Figur 5

Masse der Erde 6.0∙10²⁴ [kg], Erdradius 6.4∙10³ [km]

Ich bitte um ausführliche Lösungswege (formal) und Resultaten (numerisch) als auch um die Kräfte als Vektor – Zeichnungen und Bezeichnungen zu den/auf den Figuren, speziell den Angriffspunkt der Kräfte deutlich vermerken.
Besten Dank dafür im Voraus und schöne Grüsse.

Problem/Ansatz:

Gravitation

Comments

deine Bitte ist ganz schön fordernd. Wenigstens einen Teil solltest du können und genauer sagen , was du nicht kannst.

Wir sind ja keine HA Erzeugungsmaschine und sooo spannend ist diese einfache Aufgabe ja auch nicht. Also sag deine Probleme genauer und warum da nichts von dir kommt.

---

Hallo „lul“,
bezüglich Ihrer Bemerkungen: Ich habe einfach die Aufgabe gesamt/ganz durchgegeben, damit Sie die totale Übersicht über die Aufgabestellungen haben.
Ich habe Problem mit: „a2)“, „a3)“ bzw. „a31), a32)“ und „a4)“
Bitte um Unterstützung.
Freundliche Grüsse

Answer 1

Berechnen Sie die Grösse der Gewichtskraft FG

Nutze die Formel die eine Zeile darüber steht

FG = m∙g

Setze m und g ein die gegeben sind und berechne damit FG.

Erkläre uns dann bitte ganz genau wobei du da Probleme hast?

Comments

Hallo „Der_Mathecoach“,
bezüglich Ihrer Bemerkungen: Ich habe einfach die Aufgabe gesamt/ganz durchgegeben, damit Sie die totale Übersicht über die Aufgabestellungen haben.
Übungen „a1)“ und „b)“ wusste ich zu lösen – dennoch danke für Ihre Antwort – aber ich habe Problem mit den Übungen: „a2)“, „a3)“ bzw. „a31), a32)“ und „a4)“.
Bitte um Ihre Unterstützung.
Freundliche Grüsse