Hallo,
hier die Antwort auf Deine Frage:
"Habe das mit der Resonanzfrequenz noch nicht verstanden. Was ist das überhaupt genau?“
Der Begriff Resonanz bedeutet einfach nur Mitschwingen. Bei einem Serienschwingkreis z.B. bedeutet ist das, das hin- und her Schwingen von elektrischer Energie in einer Kapazität C und magnetischer Energie in einer Induktivität L.
Der Strom der dabei fließt lässt sich wie folgt berechnen.
Die Maschengleichung für den Serienschwingkreis lautet:
\(\frac{1}{C} * \int \limits_{}^{}i(t)dt + L * \frac{di}{dt} = 0\)
Das ist eine homogene lineare Differenzialgleichung mit konstanten Koeffizienten. Wie man solche Gleichungen löst lernen die Studenten in der Vorlesung Mathematik. Die Lösung dieser Differenzialgleichung ist eine Gleichung für den Strom i(t), den man auch Eigenschwingung des Stroms bezeichnet. Interessant dabei ist, dass dieser Strom einen rein sinusförmigen Verlauf hat. Da in unserem idealisierten Beispiel keine Verluste vorhanden sind, schwingt diese Energie in alle Ewigkeit zwischen der Kapazität und der Induktivität hin und her. Damit dürfte der Begriff Resonanz (also Schwingen) geklärt sein. Jetzt muss nur noch der Begriff Resonanzfrequenz geklärt werden.
Resonanzfrequenz ist die Antwort auf die Frage wie schnell bzw. wie oft dieser Energieaustausch in einer Zeiteinheit (z.B. Sekunde) stattfinden. Diese Häufigkeit, also die Resonanzfrequenz, lässt sich leicht berechnen. Dazu reicht die Schulmathematik.
Der induktive Blindwiderstand \(X_{L}\) errechnet sich zu
\(X_{L} = jωL\) d.h. \(X_{L}\) steigt linear mit der Frequenz an, ist also eine Geradengleichung (siehe Bild)
Der kapazitive Blindwiderstand \(X_{C}\) errechnet sich zu
\(X_{C} = \frac{1}{jωC}\) d.h. \(X_{C}\) hat die Form einer Hyperbel, da die Frequenz \(ω\) im Nenner steht (siehe Bild).
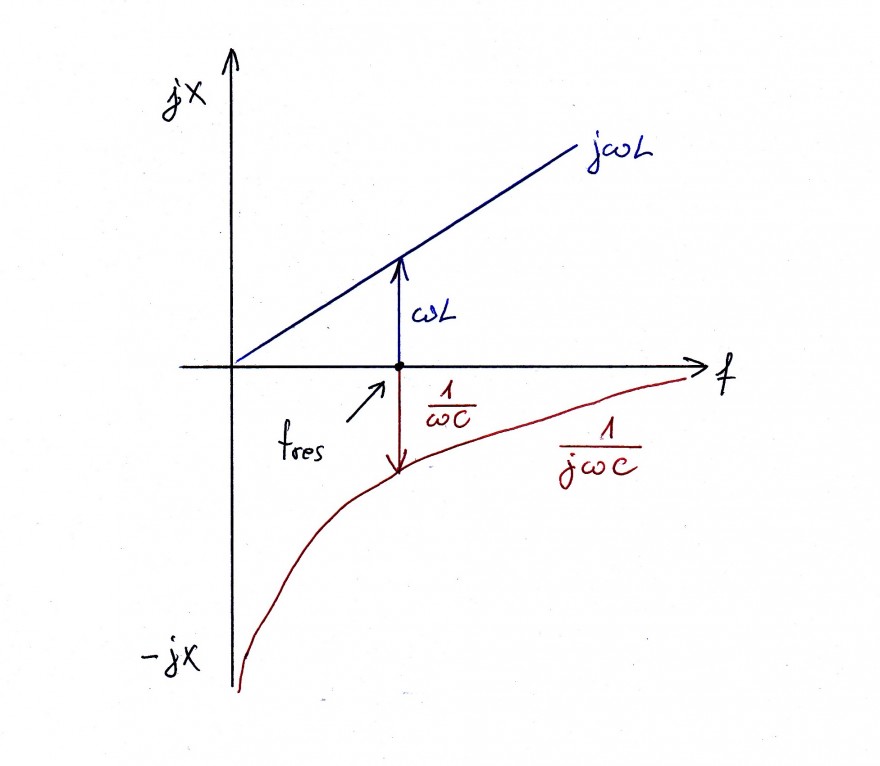
Interessant ist nun die Frage bei welcher Frequenz sind \(X_{L}\) und \(X_{C}\) gleich groß, genauer gesagt bei welcher Frequenz haben beide den gleichen Betrag. Denn bei dieser Frequenz heben sich beide auf, da \(X_{L}\) und \(X_{C}\)verschiedene Vorzeichen haben. Diese Frequenz lässt sich einfach berechnen, indem man \(X_{L}\) und \(X_{C}\) gleich setzt.
\(X_{L} = X_{C}\)
\(ωL = \frac{1}{ωC}\) löst man diese Gleichung nach \(ω\) auf erhält man
\(ω = \frac{1}{\sqrt{LC}}\) bzw.
\(f_{Res} = \frac{1}{2π\sqrt{LC}}\) das ist die Resonanzfrequenz
Mit dieser Gleichung lässt sich also ausrechnen wie oft bei einer beliebigen Induktivität L und einer beliebigen Kapazität C in einer Sekunde dieser Energieaustausch stattfindet, also welche Resonanzfrequenz dieser Schwingkreis hat.
Bei der Resonanzfrequenz ist der Gesamtwiderstand (Impedanz) Null, hat also dort eine Nullstelle. Analog gilt das Gleiche beim Parallelschwingkreis. Dort ist bei der Resonanzfrequenz der Gesamtleitwert Null. Da der Gesamtleitwert invertiert wieder ein Widerstand ergibt, befindet sich bei der Resonanzfrequenz eine Polstelle.
Alles klar? Prima!
Gruß von hightech