Hallo,
da die Brückendiagonale A - B nicht belastet ist, lässt sich der Widerstand R2 durch zweimalige Anwendung der Spannungsteilerregel leicht berechnen. Als Ergebnis erhält man:
Für UAB = +1V$$R_{2} = 1601,97 Ω$$
Für UAB = -1V$$R_{2} = 545,44 Ω$$
Hier die Berechnung:
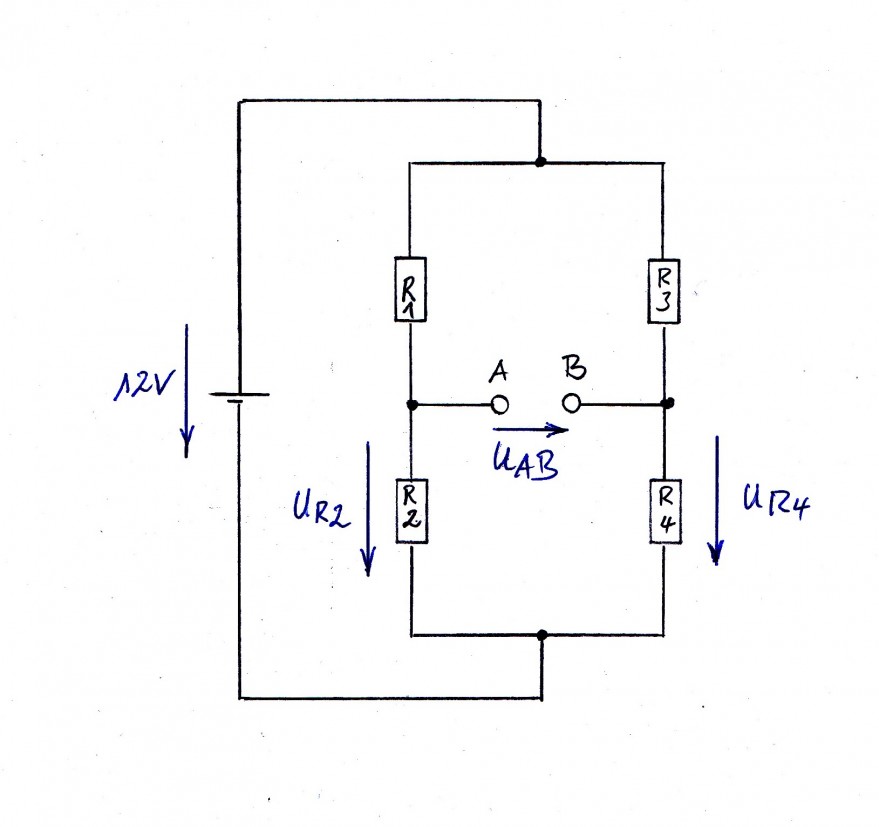
R3 und R4 bilden eine unbelasteten Spannungteiler. Mit der Spannungsteileregel lässt sich die Spannung über R4 berechnen:$$U_{R4} = 12V * \frac{R_{4}}{R_{3}+R_{4}} = 9,551 V$$
Die Spannung zwischen A und B beträgt dann +1V, wenn die Spannung UR2 um 1V größer ist als die Spannung UR4 . Also beträgt UR2 = 10,551V. Auch R1 und R2 bilden einen unbelasteten Spannungsteiler, sodass UR2 ebenfalls mir der Spannungsteilerregel berechnet werden kann. Stellt man die Gleichung der Spannungteilerregel nach R2 um erhält man:$$R_{2} = \frac{U_{R2}}{12V-U_{R2}}*R_{1} = \frac{10,551V}{12V-10,551V} * 220Ω$$
$$R_{2} = 1601,97 Ω$$
Auf die gleiche Weise lässt sich R2 berechnen, wenn die Spannungs zwischen A und B -1V betragen soll. Als Ergebnis erhält man:
$$R_{2} = 545,44 Ω$$
Gruß von hightech