Berechnen Sie den Abwurfwinkel.

Question

Aufgabe:

17 Die Flugbahn eines schräg geworfenen Balles lässt sich näherungsweise durch eine Parabel beschreiben. Bei einem Versuch betrug die Wurfweite 45 m, die maximal erreichte Höhe über dem Erdboden 22 m.

a) Berechnen Sie den Abwurfwinkel. Gehen Sie vereinfachend davon aus, dass der Abwurf in Höhe 0 erfolgte.
Problem/Ansatz:

Answer 1

Hallo Shila,

die Scheitelpunktsform der Wurfparabel y = a · (x - x_s)² + y_s lautet mit dem Scheitelpunkt S(45/2 | 22)

y = a · (x - 22,5)² + 22

Den Wert von a erhältst du durch Einsetzen des Punktes (x|y) = (0|0):

0 = a · (0 - 22,5)² + 22    →  a = - 88/2025   →   Parabel y = - 88/2025 · (x - 22,5)² + 22

Den Abwurfwinkel α erhält man mit der Tangentensteigung in (0|0):

y' = 88·(45 - 2·x)/2025  →  y' (0) =    tan(α) = 88/45 →  α ≈ 62,92°

Nachtrag:

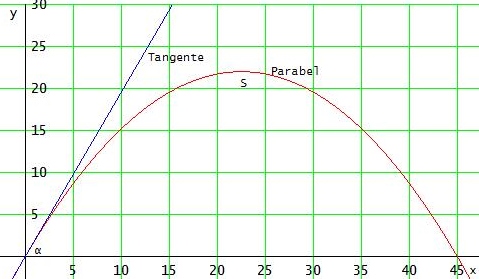
Gruß Wolfgang

Comments

Omg Danke sehr. Sie haben mich gerettet

---

gern geschehen

Answer 2

Hallo

von der Parabel kennst du die Nullstellen und Scheitel, dessen x-Koordinate in der Mitte der Nullstellen liegt. also schreib die du hast da die Parabel durch 0 geht die Formel y=ax^2+bx

y(45/2)=22 y(45)=0 damit 2 Gleichungen für a und b

und tan des Winkels y'(0) also b

Wenn die Aufgabe aus Physik stammt, hattet ihr wahrscheinlich den schiefen Wurf und du benutzt die dort entwickelten Formeln.

Gruß lul

Comments

Also 2 ist die Lösung?

---

versteh ich nicht, der Abwurfwinkel ist nicht 2.

---

Danke sehr für die Hilfe