Aufgabe:

Text erkannt:
1. Wie groß ist die de-BROGLIE-Wellenlánge fur
a) einen Körper der Masse \( m=1 \mathrm{~g} \) und der Geschwindigkeit \( v=10 \mathrm{~m} / \mathrm{s} \)
b) eines Wasserstoffmoleküls der Masse \( m_{H_{2}}=3,34 \cdot 10^{-24} \mathrm{~g} \) und der (thermischen) Geschwindigkeit \( y=1800 \mathrm{~m} / \mathrm{s} \)
c) eines Protons der Masse \( m_{p}=1,67 \cdot 10^{-24} \mathrm{~g} \) und einer Geschwindigkeit \( v=100000 \mathrm{~km} / \mathrm{s}\left(=\frac{1}{3} \mathrm{c}\right) \)
d) eines Elektrons der Masse \( m_{e}=9,1 \cdot 10^{-28} \) g und der Geschwin digkeit \( v=100000 \mathrm{~km} / \mathrm{s} \).
a) \( \frac{h}{0,001 g * 10 m * s} * \sqrt{1-\frac{10 m * s^{2}}{c^{2}}}=6,626 * 10^{-32} \mathrm{~J} / \mathrm{m} \)
b) \( \frac{h}{0,00334 g * 10^{-24} * 1800 m / s} * \sqrt{1-\frac{1800 m * s^{2}}{c^{2}}}=1,102 * 10^{-34} \mathrm{~J} / \mathrm{m} \)
c) \( \frac{h}{0,00167 g * 10^{-24} * 100000000 \mathrm{~m} / \mathrm{s}} * \sqrt{1-\frac{100000000 \mathrm{~m} * s^{2}}{c^{2}}}=3,74 * 10^{-39} \mathrm{~J} / \mathrm{m} \)
d) \( \frac{h}{0,0091 g * 10^{-28} * 100000000 m / s} * \sqrt{1-\frac{100000000 m * s^{2}}{c^{2}}}=6,864^{*} 10^{-40} J / m \)
Text erkannt:
1. Wie groß ist die de-BROGLIE-Wellenlánge fur
a) einen Körper der Masse \( m=1 \mathrm{~g} \) und der Geschwindigkeit \( v=10 \mathrm{~m} / \mathrm{s} \)
b) eines Wasserstoffmoleküls der Masse \( m_{\mathrm{H}_{2}}=3,34 \cdot 10^{-24} \mathrm{~g} \) und der (thermischen) Geschwindigkeit \( \%=1800 \mathrm{~m} / \mathrm{s} \)
c) eines Protons der Masse \( m_{p}=1,67 \cdot 10^{-24} \mathrm{~g} \) und einer Geschwindigkeit \( v=100000 \mathrm{~km} / \mathrm{s}\left(=\frac{1}{3} \mathrm{c}\right) \)
d) eines Elektrons der Masse \( m_{e}=9,1 \cdot 10^{-28} \) g und der Geschwin digkeit \( v=100000 \mathrm{~km} / \mathrm{s} \)
a) \( \frac{h}{0,001 g * 10 m * s} * \sqrt{1-\frac{10 m * s^{2}}{c^{2}}}=6,626 * 10^{-32} J / m \)
b) \( \frac{h}{0,00334 g * 10^{-24} * 1800 m / s} * \sqrt{1-\frac{1800 m * s^{2}}{c^{2}}}=1,102 * 10^{-10} \mathrm{~J} / \mathrm{m} \)
c) \( \frac{h}{0,00167 g * 10^{-24} * 100000000 m / s} * \sqrt{1-\frac{100000000 m * s^{2}}{c^{2}}}=3,239^{*} 10^{-15} \mathrm{~J} / \mathrm{m} \)
d) \( \frac{h}{0,0091 g * 10^{-28} * 100000000 m / s} * \sqrt{1-\frac{100000000 m * s^{2}}{c^{2}}}=5,944^{*} 10^{-12} J / m \)
Problem/Ansatz:
Ist das so Richtig? im Formel buch steht nur, dass nur diese 2 Formeln gelten: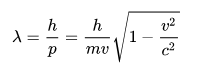
Text erkannt:
\( \lambda=\frac{h}{p}=\frac{h}{m v} \sqrt{1-\frac{v^{2}}{c^{2}}} \)