Aufgabe:
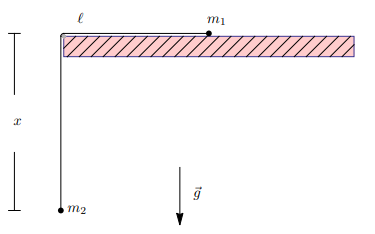
Zwei Massenpunkte mit Masse \( m_{1} \) bzw. \( m_{2} \) sind durch ein Seil der Länge \( \ell \) miteinander verbunden. Die Masse \( m_{1} \) gleitet auf einer horizontalen Unterlage, während die Masse \( m_{2} \) im homogenen Schwerefeld mit der Beschleunigung \( g \) senkrecht nach unten fällt. Die Masse des Seils und Reibungseffekte sind zu vernachlässigen.
Geben Sie für dieses System die Lagrangefunktion an, wobei zweckmäßigerweise die in der Abbildung angegebene Länge \( x \) als generalisierte Koordinate verwendet wird. Integrieren Sie die Euler-Lagrange-Gleichung mit der Anfangsbedingung
\( x(0)=0, \quad \dot{x}(0)=0 \)
Geben Sie die Zeit \( t_{0} \) an, zu der die Masse \( m_{1} \) von der horizontalen Unterlage herunterrutscht.
Ich weiß nicht, wie ich das lösen muss mithilfe der Lagrangefunktion. Wisst ihr, wie ich hier vorzugehen habe?
Was mir zu diesen Funktionen bekannt ist, ist, dass die Beschreibung der Dynamik durch eine Lagrangefunktion ist nicht immer möglich, da nicht alle Kräfte sich aus einem Potential herleiten lassen. Für einen Massenpunkt in einem nichtkonservativen Kraftfeld (also in einem Vektorfeld F(r) , dessen Rotation nicht verschwindet) geht das z.B. nicht.