Hallo WURST 21,
hier zwei Lösungsvorschläge:
Vorschlag 1:
Die Widerstände der Sternschaltung RA , RB und R1 in eine äquivalente Dreieckschaltung umrechnen. Anschließend die Widerstände zusammenfassen und Rges ausrechnen.
Vorschlag 2:
Die Widerstände der Sternschaltung RC , RB und R2 in eine äquivalente Dreieckschaltung umrechnen. Anschließend auch hier die Widerstände zusammenfassen und Rges ausrechnen.
Gruß von hightech
Hier die Lösung zum Vorschlag 1:
Wie in Bild 1 gezeichnet, lassen sich die Widerstände RA RB und R1 in eine äquivalente Dreieckschaltung mit den Widerständen RD1, RD2 und RD3 umrechnen. Als Ergebnis erhält man:
$$R_{D1} = \frac{R_{1}*R_{B}}{R_{A}} + R_{1} + R_{B}$$
$$R_{D2} = \frac{R_{1}*R_{A}}{R_{B}} + R_{1} + R_{A}$$
$$R_{D3} = \frac{R_{A}*R_{B}}{R_{1}} + R_{A} + R_{B}$$
Bild 1
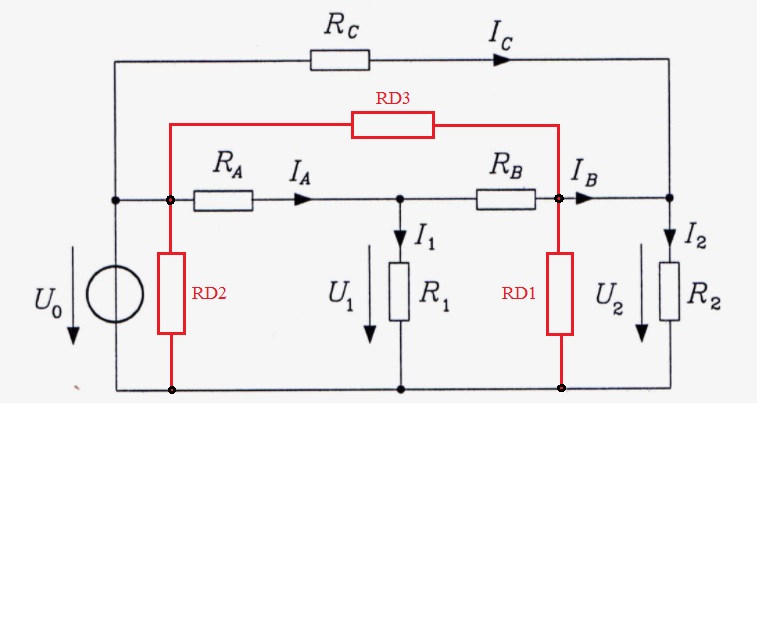
Die Widerstände lassen sich zusammenfassen und Rges ausrechnen, Bild 2:
$$R_{ges} = R_{D2} || [(R_{C}||R_{D3}) + (R_{2}||R_{D1})]$$
Bild 2
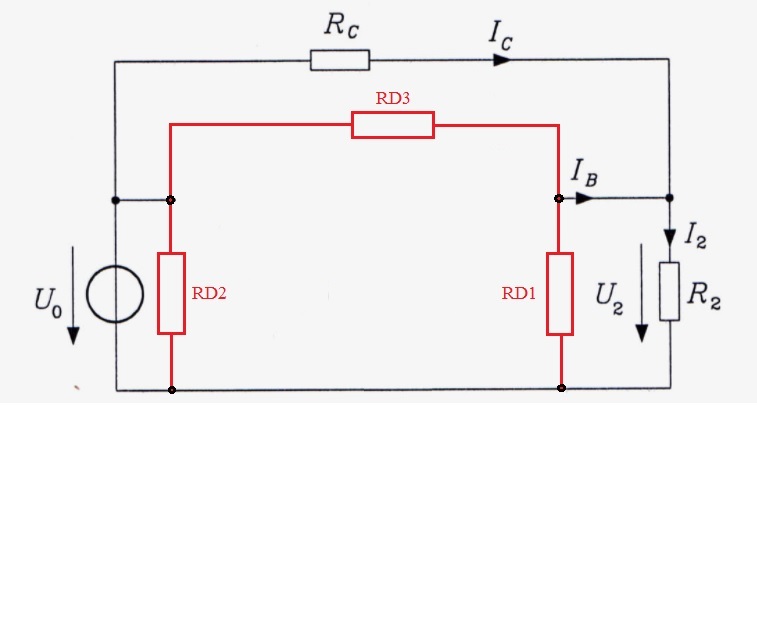
Gruß von hightech